Bài tập 2 : Cho góc xOy khác góc bẹt, lấy các điểm I, K thuộc Ox sao cho Oy < OK, lấy các điểm D, E thuộc OI sao cho OI = OD, OK = OE. Gọi A là giao điểm của KD và IE.
a. Chứng minh: IE = KB
b. Chứng minh: Tam giác AIK và tam giác ADE
c. Chứng minh: OA là tia phân giác góc xOy

 (hai góc tương ứng)
(hai góc tương ứng)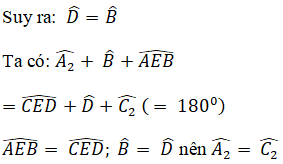
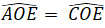 (hai góc tương ứng)
(hai góc tương ứng)
a: Xét ΔODK và ΔOIE có
OD=OI
\(\widehat{DOK}\) chung
OK=OE
Do đó: ΔODK=ΔOIE
Suy ra: DK=IE
b: XétΔAIK và ΔADE có
\(\widehat{AIK}=\widehat{ADE}\)
IK=DE
\(\widehat{AKI}=\widehat{AED}\)
DO đó: ΔAIK=ΔADE