Cho góc xAy khác góc bẹt , trên tia Ax lấy điểm B, E tren tia Ay lấy điểm D, C sao cho AB=AD, BE = DC. Gọi O là giao điểm của BC và DE. Chứng minh:
a/ \(\Delta ABC=\Delta ADE\)
b/ \(\Delta BOE=\Delta DOC\)
c/ AO là tia phân giác của góc xAy
d/ \(AO\perp BD\) ( gợi ý: gọi H là giao điểm của AO và BD)

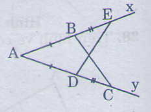
a) Ta có AE = AB + BE
AC = AD + DC
mà AB = AD (gt)
BE = DC (gt)
=> AE = AC
Xét 2 tam giác ABC và tam giác ADE có :
AB = AD (gt)
AE = AC (cmt)
A là góc chung
=> tam giác ABC = tam giác ADE (c-g-c)
b) Ta có : góc B1 + góc B2 = 180 độ
góc D1 + góc D2 = 180 độ
mà góc B1 = góc D1 (vì tam giác ABC = tam giác ADE)
=>góc B2 = góc D2
Xét 2 tam giác BOE và tam giác DOC có :
góc B2 = góc D2 (cmt)
góc E = góc C (vì tam giác ABC = tam giác ADE )
BE = DC (gt)
=> tam giác BOE = tam giác DOC (g-c-g)
c)Xét 2 tam giác ABO và tam giác ADO có:
AO là cạnh chung
AB = AD (gt)
BO = DO (vì tam giác BOE = tam giác DOC)
=>tam giác ABO = tam giác ADO (c-c-c)
=> góc A1 = góc A2 (2 góc tương ứng)
=> AO là tia phân giác của góc xAy
d) Xét 2 tam giác ABH và tam giác ADH có:
AH là cạnh chung
AB = AD (gt)
góc A1 = góc A2 (cm ở câu c)
=> tam giác ABH =tam giác ADH (c-g-c)
=> góc H1 = góc H2 (2 góc tương ứng)
mà góc H1 + góc H2 = 180 độ
=> góc H1 = góc H2 = 180/2= 90 độ
=> AH vuông góc với BD
Bạn vẽ x và y vào hình nhé, mình quên kí hiệu vào hình!