giá trị nhỏ nhất của Q=a2+4b2-10a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C
1
C
2
7 tháng 8 2021
a) Ta có: \(M=-x^2-4x+20\)
\(=-\left(x^2+4x-20\right)\)
\(=-\left(x^2+4x+4-24\right)\)
\(=-\left(x+2\right)^2+24\le24\forall x\)
Dấu '=' xảy ra khi x=-2
NT
0
NH
1
28 tháng 11 2016
\(Q=a^2+4b^2+10a=a^2+2.a.5+25-25+\left(2b\right)^2=\left(a+5\right)^2+\left(2b\right)^2+\left(-25\right)\)
\(\left(a+5\right)^2\ge0;\left(2b\right)^2\ge0=>\left(a+5\right)^2+\left(2b\right)^2\ge0=>\left(a+5\right)^2+\left(2b\right)^2+\left(-25\right)\ge0\)
Vậy GTNN của Q là - 25. Dấu "=" xảy ra khi a + 5 = 0 => a = -5 và 2b = 0 => b = 0
NT
2
15 tháng 12 2016
\(Q=a^2-10a+25-25+4b^2\)
\(Q=\left(a^2-2.5.a+5^2\right)+4b^2-25=\left(a-5\right)^2+4b^2-25\)
\(Q\ge-25\) đẳng thức khi \(\hept{\begin{cases}a=5\\b=0\end{cases}}\)
15 tháng 12 2016
Q=a2+4b2-10a
=a2-10a+25-25+4b2
=(a-5)2+4b2-25
\(\Rightarrow\left(a-5\right)^2+4b^2\ge0\) voi moi a
\(\Leftrightarrow\left(a-5\right)^2+4b^2\ge-25\)
Vay GTNN la -25
Dau "=" xay ra khi : a-5=0 \(\Rightarrow\)a=5
4b=0 \(\Rightarrow\)b=0
CM
2 tháng 7 2019
Điều kiện x ≠ 2 và x ≠ 0
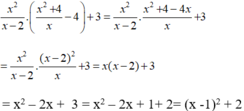
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.
Q=a^2+4b^2-10a
Q=a^2-5a-5a+25+4b^2-25
Q=a(a-5)-5(a-5)+4b^2-25
Q=(a-5)^2+4b^2-25 >=-25
Dấu "=" xảy ra khi a-5=0;b=0
<=> a=5;b=0
Vậy Min Q=-25 khi a=5;b=0
a2+4b2-10a
=a2-10a+4b2
=a2-10a+25+4b2-25
=(a-5)2+4b2-25
Vì (a-5)2>=0 với mọi a.Dấu bằng xảy ra khi a-5=0
<=> a =5
Lại có 4b2>=0 với mọi b.Dấu bằng xảy ra khi 4b2=0
<=> b2 =0
<=> b =0
=>(a-5)2+4b2-25>=-25 với mọi a;b.Dấu bắng xảy ra khi a=5;b=0
Vậy giá trị nhỏ nhất của Q là -25 tại a=5;b=0