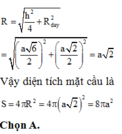Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, cạnh bên SC tạo với mặt đáy một góc 60 độ. Diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 12 2016
mình nghĩ câu hỏi của bạn chắc là nhầm thì phải.đáp án diện tích phải là:8π\(a^2\)
có phải bạn muốn tìm bán kính mặt cầu ngoại tiếp ko?nếu tìm bán kính ta làm như sau:SA=tan(60).AC=\(\sqrt{6}\)a
gọi O là tâm đáy suy ra AO=\(\frac{a\sqrt{2}}{2}\).từ O kẻ đt d vuông góc vs đáy .gọi Mlà trung điểm SA.trong mp(SAO) từ Mkẻ đt vuông góc SA cắt d tại I. I là tâm mặt cầu
R=IA=\(\sqrt{AI^2+AO^2}=a\sqrt{2}\)
CM
2 tháng 3 2019
Đáp án A.
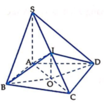
1. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD
Ta có
C B ⊥ A B , C B ⊥ S A , A B ∩ S A = A ⇒ C B ⊥ S A B ⇒ C B ⊥ S B ⇒ Δ S B C
vuông tại B.
Lại có
C D ⊥ A D , C D ⊥ S A , A D ∩ S A = A ⇒ C D ⊥ S A D ⇒ C D ⊥ S D
⇒ Δ S D C vuông tại D.
Mặt khác S A ⊥ A B C D ⇒ S A ⊥ A C ⇒ Δ S A C vuông tại A.
Gọi I là trung điểm của SC. Các tam giác: Δ S A C , Δ S B C , Δ S D C lần lượt vuông tại các đỉnh A, B và D nên I S = I A = I B = I C = I D = 1 2 S C . Vậy mặt cầu ngoại tiếp hình chóp S.ABCD có tâm I, bán kính R = 1 2 S C
2. Tính diện tích mặt cầu
Ta có S C , A B C D ^ = S C , A C ^ = S C A ^ = 60 °
Do Δ A D C vuông tại A nên S ?A C = 1 2 A D . C D ⇔ A D = 2 S Δ A D C C D = a 2 3 a = a 3
⇒ A C = A D 2 + C D 2 = a 3 2 + a 2 = 2 a
Mà A C = S C . cos S C A ^ ⇒ S C = 2 a cos 60 ° = 4 a
Vậy bán kính của mặt cầu ngoại tiếp hình chóp S.ABCD là R = S C 2 = 4 a 2 = 2 a và diện tích mặt cầu là S = 4 π R 2 = 4 π . 2 a 2 = 16 π a 2 (đvdt).
CM
7 tháng 1 2018
Đáp án A
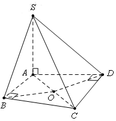
Tam giác ADC vuông tại D ⇒ S Δ A D C = 1 2 . A D . C D = a 2 3 2
⇒ C D = a 3 ⇒ A C = A D 2 + C D 2 = a 2 + a 3 2 = 2 a .
Vì tứ giác ABCD có A B C ⏜ = A D C ⏜ = 90 ∘ ⇒ A B C D là tứ giác nội tiếp đường tròn tâm O với O là trung điểm của AC ⇒ R A B C D = A C 2 = a .
Và S A ⊥ A B C D ⇒ S C ; A B C D ⏜ = S C ; A C ⏜ = S C A ⏜ = 60 ∘
Tam giác SAC vuông tại A ⇒ tan S C A ⏜ = S A A C ⇒ S A = 2 a 3 .
Suy ra bán kính mặt cầu cần tính là:
R = R 2 A B C D + S A 2 4 = 2 a ⇒ S m c = 16 π a 2 .
CM
9 tháng 4 2019
Phương pháp
Hình chóp có cạnh bên vuông góc với đáy, sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp
Hình chóp có cạnh bên vuông góc với đáy, sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp
