Một con lắc lò xo gồm lò xo nhẹ nằm ngang và mặt phẳng M. Con lắc dao động điều hòa trên trục Ox, chiều dài của lò xo thay đổi từ 20cm đến 30cm. Ở vị trí lò xo dài 30cm, độ lớn gia tốc của vật M là 8m/s2. Chọn gốc tọa độ O tại vị trí cân bằng, gốc thời gian là lúc vật M đi qua O theo chiều âm. Lấy \(\pi^2=10\)
a) Viết phương trình dao động của vật M
b) Xác định vị trí vật M khi con lắc có động năng bằng ba lần thế năng
c) Biết hiệu giữa quãng đường lớn nhất và quảng đường nhỏ nhất (vật M đi được trong cùng một khoảng thời gian \(\Delta t\)) đạt cực đại. Tính \(\Delta t\)
d) Một vật nhỏ N dao động trên trục Oy với phương trình \(y=10cos\left(4\pi t-\dfrac{\pi}{6}\right)cm\) (Ox và Oy vuông góc với nhau, O là vị trí cân bằng của cả vật N và vật M). Xác định khoảng cách giữa vật M và vật N khi vật M có li độ \(x=-2,5\sqrt{3}cm\) và đang chuyển động theo chiều âm





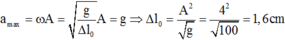
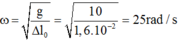
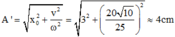


Gọi \(l\) là chiều dài lò xo lúc ko biến dạng \(\Rightarrow\left\{{}\begin{matrix}l_{max}=l+A=30\\l_{min}=l-A=20\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}l=25cm\\A=5cm\end{matrix}\right.\)
Khi lò xo dài 30cm, tức là vật đang ở biên dương, độ lớn của gia tốc là 8m/s^2\(\Rightarrow\left|a\right|=\omega^2A=800\left(cm/s^2\right)\Leftrightarrow\omega=\sqrt{\dfrac{800}{A}}=\sqrt{\dfrac{800}{5}}=4\pi\left(rad/s\right)\)
Gốc thời gian là lúc vật qua O theo chiều âm, tức là pha ban đầu bằng pi/2
\(\Rightarrow x=5\cos\left(4\pi t+\dfrac{\pi}{2}\right)\left(cm\right)\)
b/ \(W_d=3W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{3+1}}=\pm\dfrac{A}{2}\)
Nghĩa là khi vật qua vị trí có li độ là \(\left[{}\begin{matrix}x=-2,5cm\\x=2,5cm\end{matrix}\right.\)
c/ Góc vật quay được trong thời gian delta t là: \(\varphi=\omega.\Delta t=4\pi.\Delta t\left(rad\right)\)
Quãng đường lớn nhất đi được khi vật chuyển động xung quanh vtcb
\(S_{max}=2A.\sin\left(2\pi.\Delta t\right)\)
Quãng đường nhỏ nhất đi được khi vật chuyển động xung quang biên
\(S_{min}=2A-2.A\cos\left(2\pi.\Delta t\right)\)
\(\Rightarrow S_{max}-S_{min}=2A\left(\sin\left(2\pi.\Delta t\right)-1+\cos\left(2\pi.\Delta t\right)\right)\)
Xét \(M=\sin\left(2\pi.\Delta t\right)+\cos\left(2\pi.\Delta t\right)=\cos\left(2\pi\Delta t-\dfrac{\pi}{2}\right)+\cos\left(2\pi\Delta t\right)=2\cos\left(\dfrac{2\pi\Delta t-\dfrac{\pi}{2}+2\pi\Delta t}{2}\right)\cos\left(\dfrac{2\pi\Delta t-\dfrac{\pi}{2}-2\pi\Delta t}{2}\right)\)
\(M=2\cos\left(2\pi\Delta t-\dfrac{\pi}{4}\right)\cos\left(\dfrac{\pi}{4}\right)\)
Để \(\left(S_{max}-S_{min}\right)_{max}\Leftrightarrow M_{max}\Leftrightarrow\cos\left(2\pi\Delta t-\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow2\pi\Delta t-\dfrac{\pi}{4}=0\Leftrightarrow\Delta t=\dfrac{\pi}{4.2\pi}=\dfrac{1}{8}\left(s\right)\)
d/ Ta thấy vật N luôn dao động vuông pha với vật M
\(\Rightarrow\left(\dfrac{x_M}{A_M}\right)^2+\left(\dfrac{x_N}{A_N}\right)^2=1\Leftrightarrow\left(\dfrac{2,5\sqrt{3}}{5}\right)^2+\left(\dfrac{x_N}{10}\right)^2=1\Leftrightarrow x_N=\pm2,5\left(cm\right)\)
Tính khoảng cách nên ko cần quan tâm xN dương hay âm
\(MN=\sqrt{ON^2+OM^2}=\sqrt{2,5^2+\left(2,5\sqrt{3}\right)^2}=5cm\)
em cảm ơn ạ