Cho A = 21 + 22 + 23 + 24 + ... + 2100. Chứng minh rằng A chia hết cho 3.
Giúp mik ik ^^
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
0
TM
1
DD
Đoàn Đức Hà
Giáo viên
9 tháng 11 2021
\(A=2+2^2+2^3+2^4+...+2^{100}\)
\(=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{99}+2^{100}\right)\)
\(=\left(2+2^2\right)+2^2\left(2+2^2\right)+...+2^{98}\left(2+2^2\right)\)
\(=6\left(1+2^2+...+2^{98}\right)\)chia hết cho \(6\).
TN
1
AH
Akai Haruma
Giáo viên
13 tháng 12 2021
Lời giải:
$A=(2+2^2)+(2^3+2^4)+....+(2^{99}+2^{100})$
$=2(1+2)+2^3(1+2)+...+2^{99}(1+2)$
$=2.3+2^3.3+...+2^{99}.3$
$=3(2+2^3+...+2^{99})\vdots 3$
Ta có đpcm.
PD
4
23 tháng 10 2021
\(A+2+2^2+2^3+...+2^{100}\)
\(=\left(2+2^2\right)+2^2\left(2+2^2\right)+...+2^{98}\left(2+2^2\right)\)
\(=6+2^2.6+...+2^{98}.6=6\left(1+2^2+...+2^{98}\right)⋮6\)
23 tháng 10 2021
\(A=2+2^2+2^3+2^4+...+2^{100}\)
\(=2\cdot3+...+2^{99}\cdot3\)
\(=6\left(1+...+2^{99}\right)⋮6\)
LT
0
E
19 tháng 3 2021
Ta có :
\(A=2+2^2+2^3+2^4...2^{2010}\)\(^0\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{2009}\left(1+2\right)\)
\(=2.3+2^3.3+....+2^{2009}.3\)
\(=3\left(2+2^3+....+2^{2009}\right)⋮3\)
Ta có :
\(2+2^2+2^3+2^4+....+2^{2010}\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{2008}\left(1+2+2^2\right)\)
\(=2.7+2^4.7+....+2^{2008}.7\)
\(=7\left(2+2^4+....+2^{2008}\right)⋮7\)
Vậy \(2^1+2^2+2^3+2^4+...+2^{2010}⋮3\) và \(7\)
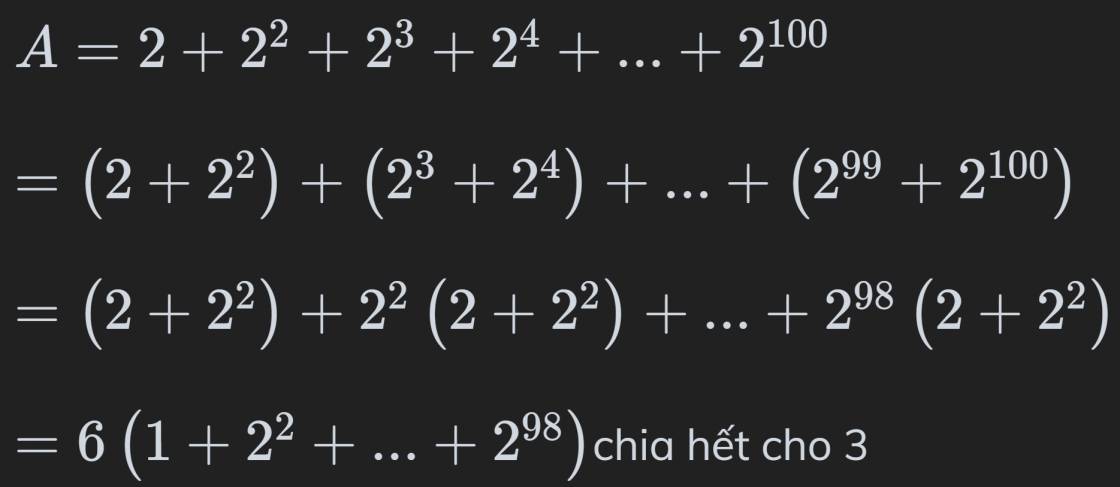
*Sửa lại đề*
A = 21+ 22+ 23+ 24 + .. + 2100
A = (21+22) + (23+ 24) +...+ (299+ 2100)
A = 2.(1+2) + 23.(1+2) + .. + 299. (1+2)
A = 2.3 + 23. 3 + .. + 299.3
A = 3 . (21 + 23 + .... + 299)
Mà 3 chia hết cho 3
=> A chia hết cho 3