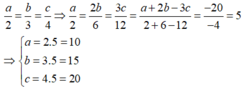tìm số nguyên dương a,b,c cho a2+b3+c4= 90
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
20 tháng 1 2018
Ta có:
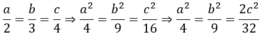
Theo tính chất dãy tỉ số bằng nhau ta có:
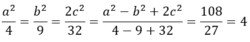
Ta có:
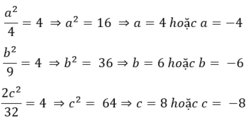
Mà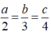 
nên a, b và c cùng dấu.
Vậy ta tìm được các số a1 = 4; b1 = 6; c1 = 8 hoặc a2 = -4; b2 = -6 và c2 = -8
PT
1
CM
7 tháng 6 2017
Ta có: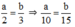 
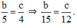
Suy ra: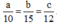 
Theo tính chất dãy tỉ số bằng nhau ta có: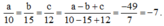 
Ta có:
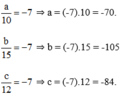
Vậy a = -70; b = -105; c = -84.
PT
1
CM
27 tháng 4 2018
Ta có: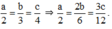 
Theo tính chất dãy tỉ số bằng nhau ta có:
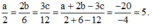
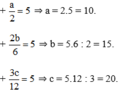
Vậy a = 10 ; b = 15 ; c = 20.
NA
1
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
Đặt \(P=\dfrac{a^3}{a^2+b^2+ab}+\dfrac{b^3}{b^2+c^2+bc}+\dfrac{c^3}{c^2+a^2+ca}\)
Ta có: \(\dfrac{a^3}{a^2+b^2+ab}=a-\dfrac{ab\left(a+b\right)}{a^2+b^2+ab}\ge a-\dfrac{ab\left(a+b\right)}{3\sqrt[3]{a^3b^3}}=a-\dfrac{a+b}{3}=\dfrac{2a-b}{3}\)
Tương tự: \(\dfrac{b^3}{b^2+c^2+bc}\ge\dfrac{2b-c}{3}\) ; \(\dfrac{c^3}{c^2+a^2+ca}\ge\dfrac{2c-a}{3}\)
Cộng vế:
\(P\ge\dfrac{a+b+c}{3}=673\)
Dấu "=" xảy ra khi \(a=b=c=673\)
HH
0
CM
11 tháng 12 2018
Đáp án A.
Phương trình mặt phẳng (Oxy): 
Lấy điểm A’ đối xứng với A qua mặt phẳng (Oxy). Dễ thấy 
Ta có: 
Dấu bằng xảy ra khi và chỉ khi M nằm giữa A’B, hay M là giao điểm của A’B với mặt phẳng (Oxy).
Đường thẳng A’B có 
và qua 
phương trình đường thẳng A’B:
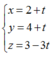
M là giao của A’B và (Oxy) nên 
Do đó 
CM
30 tháng 8 2019
Đáp án A.
Phương trình mặt phẳng (Oxy):
z = 0 ⇒ c = 0.
Lấy điểm A’ đối xứng với A qua mặt phẳng (Oxy). Dễ thấy
A ' 5 ; 7 ; − 6 .
Ta có: M A + M B = M A ' + M B ≥ A ' B .
Dấu bằng xảy ra khi và chỉ khi M nằm giữa A’B, hay M là giao điểm của A’B với mặt phẳng (Oxy).
Đường thẳng A’B có u → = 1 ; 1 ; − 3 và qua B 2 ; 4 ; 3 ⇒ phương trình đường thẳng A’B:
x = 2 + t y = 4 + t z = 3 − 3 t .
M là giao của A’B và (Oxy) nên M 3 ; 5 ; 0 .
Do đó P = 3 2 + 5 3 − 0 4 = 134.
