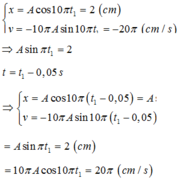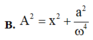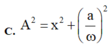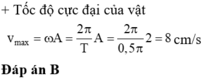một vật dao động điều hòa xung quanh vị trí cân bằng với biên độ A và vận tốc góc ω. Tại điểm có li độ x = A/2 độ lớn vận tốc là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng công thức: \(A^2=x^2+\frac{v^2}{\omega^2}\)
với \(x=\frac{A}{2}\) ta có
\(A^2=\left(\frac{A}{2}\right)^2+\frac{v^2}{\omega^2}\Leftrightarrow\frac{3A^2}{4}=\frac{v^2}{\omega^2}\Leftrightarrow v^2=\frac{3A^2}{4}.\omega^2\Rightarrow \left|v\right|=\frac{\sqrt{3}A}{2}.\omega=\frac{\sqrt{3}A}{2}.\frac{2\pi}{T}\)

Đáp án C
Tần số góc của dao động 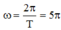
→ Thời điểm t = 0,1s ứng với góc lùi ![]()
Biểu diễn các vị trí tương ứng trên đường tròn, ta thu được:
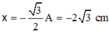
![]()
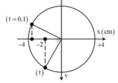

Mối liên hệ giữa li độ x và gia tốc a là a = - ω 2 x
Đáp án D

Đáp án D
+ Mối liên hệ giữa li độ x và gia tốc a là a = - ω 2 x .

Đáp án D
+ Mối liên hệ giữa li độ x và gia tốc a là A = - ω 2 x

Đáp án A.
Lời giải chi tiết:
Vận tốc của vật dao động điều hòa: v = x ' = - Aωsin ( ωt + φ )