Cho tam giác ABC có AM là đường trung trực của đoạn thawgr BC (M thuộc BC)
a) Chứng minh: tam giác AMB=tam giác AMC
b) So sánh: AB và AC; BAM và CAM; ABM và ACM
c) Lấy điểm N trên đoạn thẳng AM. CMR: tam giác ANB= Tam giác ANC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 11 2021
a
vì AM là tia phân giác của góc A=>góc BAM=CAM
xét tam giác AMB và tam giác AMC có:
góc BAM=CAM,AM chung,AB=AC=>tam giác AMB = tam giác AMC
b
vì tam giác AMB = tam giác AMC=>MB=MC=>M là trung điểm BC
vì tam giác AMB = tam giác AMC=>góc BAM=CAM mà góc BAM+CAM=180=>BAM=CAM=180 độ/2=90 độ=>AM vuông góc với BC
c
xét tam giác ABM và KCM có
MB=MC,MA=MK,góc BMA=CMK(vì đối đỉnh)=>tam giác ABM = KCM=>AB=CK
vì tam giác ABM = KCM=>góc ABM=KMB mà 2 góc trên ở vị trí so le trog=>AB//CK
KV
11 tháng 3 2023
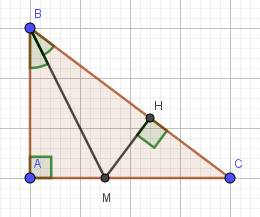
a) Xét hai tam giác vuông: \(\Delta AMB\) và \(\Delta HMB\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{HBM}\) (do BM là phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta AMB=\Delta HMB\) (cạnh huyền-góc nhọn)
b) Do \(\Delta AMB=\Delta HMB\) (cmt)
\(\Rightarrow AM=HM\) (hai cạnh tương ứng)
c) \(\Delta MHC\) vuông tại H
\(\Rightarrow MC\) là cạnh huyền nên là cạnh lớn nhất
\(\Rightarrow HM< MC\)
Lại có HM = AM (cmt)
\(\Rightarrow AM< MC\)
HQ
14 tháng 12 2017
a, +Xét tam giác ABM và ACM có:
AB=AC(Giả thiết) --
AM là cạnh chung) I =>tam giác ABM=ACM (C-C-C)
MB=MC(Giả thiết) --
b, +Ta có: tam giác ABM=ACM
=> góc AMB=góc AMC (2 góc tương ứng)
+Ta có:
góc AMB+AMC=180 ( 2 góc kề bù)
AMB+AMB=180
AMB = 90(độ)
=>AM vuông góc với BC
c, +Ta có: tam giác ABM=ACM
=> góc BAM=góc CAM(2 góc tương ứng)
=>AM là tia phân giác của góc BAC
hay AM là tia phân giác của góc A
Vậy a,tam giác ABM=ACM
b,AM vuông góc với BC
c,AM là tia phân giác của góc A
BC.
16 tháng 6 2023
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
c: BM=CM=3cm
=>AM=4cm
a). Ta có AM là đường trung trực của đoạn thẳng BC => AM\(\perp\) BC và BM=CM
Xét tam giác AMB vuông tại M và tam giác AMC vuông tại M có:
AM là cạnh chung.
BM=CM (cmt)
=> Tam giác AMB=tam giác AMC (hai cạnh góc vuông)
b). Tam giác AMB=tam giác AMC
=> AB=AC (hai cạnh tương ứng)
=> \(\widehat{BAM}\) = \(\widehat{CAM}\) (hai góc tương ứng)
=> \(\widehat{ABM}=\widehat{ACM}\) (hai góc tương ứng)
c). Xét tam giác ANB và tam giác ANC có:
AB=AC (cmt)
\(\widehat{BAN}=\widehat{CAN}\) (\(\widehat{BAM}=\widehat{CAM};N\in\) AM)
AN là cạnh chung.
=> Tam giác ANB=tam giác ANC (c.g.c)