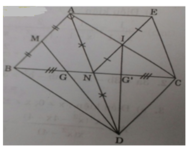
Cho tam giác ABC vuông tại A .Gọi M,N lần lượt là trung điểm của AB, AC.
a) Chứng minh: Tứ giác BMNC là hình thang
b) BN và CM cắt nhau tại G. Gọi E và F lần lượt là trung điểm của BG và GC.Chứng minh : Tứ giác MNEF là hình bình hành
c) Tia AG cắt BC tại H.Chứng minh: Tứ giác AMHN là hình chữ nhật
d) Gọi K là điểm đối xứng với điểm M qua N và I là trung điểm của NH.
Chứng minh : HN,MC,BK đồng quy tại 1 điểm

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2(1)
hay BMNC là hình thang
b: Xét ΔGBC có
E là trung điểm của GB
F là trung điểm của GC
Do đó: EF là đường trung bình
=>EF//BC và EF=BC/2(2)
Từ (1) và (2) suy ra MN//FE và MN=FE
hay MNEF là hình bình hành
c: Xét ΔABC có
BN,CM là các đường trung tuyến
BN cắt CM tại G
Do đó: G là trọng tâm của ΔABC
mà AG cắt BC tại H
nên H là trung điểm của BC
Xét ΔABC có
H là trung điểm của BC
M là trung điểm của BA
Do đó: HM là đường trung bình
=>HM//AC và HM=AC/2
=>HM=AN và HM//AN
=>AMHN là hình bình hành
mà \(\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật