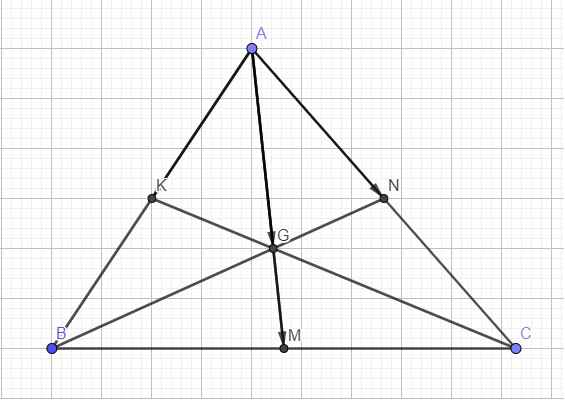
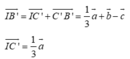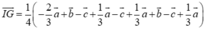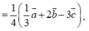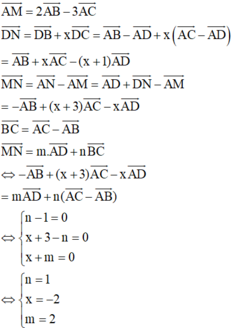Cho tam giác ABC có g là trọng tâm.gọi M,N là các điểm xác định bởi AM=2AB ,AN=2/5AC. phần tích véc tơ GM theo véc tơ GA và GB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 10 2021
Theo tính chất trọng tâm ta có: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
Mặt khác AM là trung tuyến nên: \(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)\Rightarrow3\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{AC}\) (1)
K là trung điểm AB, N là trung điểm AC nên: \(\left\{{}\begin{matrix}\overrightarrow{AK}=\dfrac{1}{2}\overrightarrow{AB}\\\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=2\overrightarrow{AK}\\\overrightarrow{AC}=2\overrightarrow{AN}\end{matrix}\right.\) (2)
(1);(2) \(\Rightarrow3\overrightarrow{AG}=2\left(\overrightarrow{AK}+\overrightarrow{AN}\right)\)
CM
9 tháng 1 2018
Đáp án C
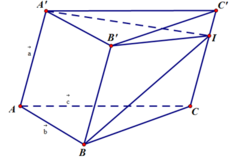
A M → = 2 A B → − 3 A C → D N → = D B → + x D C → = A B → − A D → + x A C → − A D → = A B → + x A C → − ( x + 1 ) A D → M N → = A N → − A M → = A D → + D N → − A M → = − A B → + ( x + 3 ) A C → − x A D → B C → = A C → − A B →
Để 3 vectơ A D → , B C → , M N → đồng phẳng ⇔ ∃ m , n ∈ R sao cho :
A M → = 2 A B → − 3 A C → D N → = D B → + x D C → = A B → − A D → + x A C → − A D → = A B → + x A C → − ( x + 1 ) A D → M N → = A N → − A M → = A D → + D N → − A M → = − A B → + ( x + 3 ) A C → − x A D → B C → = A C → − A B → M N → = m . A D → + n B C → ⇔ − A B → + ( x + 3 ) A C → − x A D → = m A D → + n ( A C → − A B → ) ⇔ n − 1 = 0 x + 3 − n = 0 x + m = 0 ⇔ n = 1 x = − 2 m = 2
