Cho hình thoi ABCD có góc A = 1200 ; kẻ AE vuông góc với CD ; AF vuông góc với BC. Chứng minh tam giác AEF đều
các bn vẽ giúp mink hình lun nha
mink cảm ơn các bn trước
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
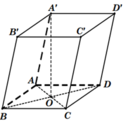
Gọi O = AC ∩ BD.Từ giả thiết suy ra A'O ⊥ ABCD
Cũng từ giả thiết, suy ra ABC là tam giác đều nên
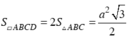
Đường cao khối hộp
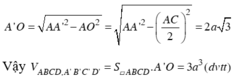

a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: (SC;(ABCD))=(CS;CA)=góc SCA
Xét ΔBAC có BA=BC vàgóc BAC=60 độ
nên ΔBAC đều
=>AC=a
=>\(SC=\sqrt{SA^2+AC^2}=\dfrac{\sqrt{10}}{3}\cdot a\)
tan SCA=SA/AC=1/3
=>góc SCA=18 độ

\(AB=\dfrac{BH}{\sin A}=\dfrac{1,5}{\sin30^0}=3\left(cm\right)\)
Do đó \(P_{ABCD}=4AB=12\left(cm\right)\)

Kẻ BH vuông góc AD
Tam giác ABH là tam giác đều nên BH=AD=10(cm)
Suy ra SABCD=10.10=100(cm2)
Xét tứ giác AECF có
\(\widehat{AEC}+\widehat{AFC}=180^0\)
Do đó: AECF là tứ giác nội tiếp
Suy ra: \(\widehat{EAF}=180^0-120^0=60^0\)
Xét ΔEAC vuông tại E và ΔFAC vuông tại F có
CA chung
\(\widehat{ECA}=\widehat{FCA}\)
Do đó: ΔEAC=ΔFAC
Suy ra: AE=AF
hayΔAEF cân tại A
mà \(\widehat{FAE}=60^0\)
nên ΔAEF đều