Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. Chọn A làm mốc, chọn thời điểm xuất phát của hai xe làm mốc thời gian và chọn nhiều chuyển động của hai xe là chiều dương.
Phương trình xe 1: \(x_1=x_{0_1}+v_1t=54t\)
Phương trình xe 2: \(x_2=x_{0_2}+v_2t=10+48t\)
b. Hai xe gặp nhau thì: \(x_1=x_2\Leftrightarrow54t=10+48t\Rightarrow t=\dfrac{5}{3}\left(h\right)\)
Vị trí gặp nhau cách A: \(x_1=54.\dfrac{5}{3}=90\left(km\right)\)
Chọn D.
Cách 2: Mỗi giờ xe A đi được nhiều hơn xe B là 54 - 48 = 6km.
Muốn xe A đi được nhiều hơn xe B là 12km thì phải cần thời gian: 12/6 = 2h.
Lúc này, xe A đi được: AC = 54.2 = 108km.
Đáp án C
Chọn trục Ox trùng với đường AB, gốc O tại A, chiều dương hướng từ A sang B, gốc thời gian là lúc hai xe xuất phát
Phương trình chuyển động của ô tô chạy từ A:
(km)
Phương trình chuyển động của ô tô chạy từ B:
(km)
Khi hai ô tô gặp nhau thì
Chú ý: Khi hai vật cùng chuyển động dọc theo Ox chúng gặp nhau khi: x A = x B
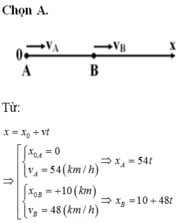
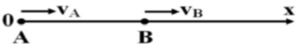
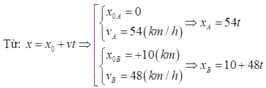
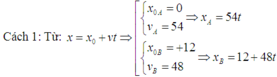
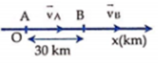
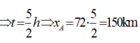
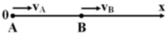
Tóm tắt
\(S_{AB}=10km\)
\(V_1=54km\)/\(h\)
\(V_2=48km\)/\(h\)
____________
\(a\)) \(t=?\)
\(b\)) \(S_{AC}=?\)
Giải
a)
Gọi \(t_1;t_2\) lần lượt là thời gian đi của người đi vận tốc 54 km/h và 48 km/h.
Ta có:
\(S_{AC}-S_{BC}=S_{AB}=10\Rightarrow V_1.t_1-V_2.t_2=10\)
Trong đó: \(t_1=t_2=t;V_1=54km\)/\(h;V_2=48km\)/\(h\).
\(\Rightarrow10=54.t-48t=t\left(54-48\right)=6t\Rightarrow t=\frac{10}{6}=\frac{5}{3}\left(h\right)\)
b) \(\Rightarrow S_{AC}=54.\frac{5}{3}=90\left(km\right)\)
Vậy nơi 2 người gặp nhau cách điểm A là 90 km
Cảm ơn nhé