Một xe máy xuất phát từ A lúc 6h và chạy với vận tốc 40km/h để đến B. Một ô tô xuất phát từ B lúc 8h và chạy với vận tốc 80km/h theo cùng chiều với xe máy. Coi chuyển động của ô tô và xe máy là thẳng đều. Khoảng cách AB là 20km.
a) Sau bao lâu thì ô tô đuổi kịp xe máy?
b) Chỗ gặp nhau cách A bao xa?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Công thức tính quãng đường đi được và phương trình chuyển động
- Của xe máy xuất phát lúc 6 giờ:
s 1 = v 1 t = 40t;
x 1 = s 1 = 40t (với x0 = 0 )
- Của ô tô xuất phát lúc 8 giờ :
s 1 = v 2 (t – 2) = 80(t – 2) với t ≥ 2;
x 2 = x 0 + s 2 = 20 + 80(t – 2)

Kiểm tra lại kết quả thu được nhờ đồ thị bằng cách giải phương trình:
x 1 = x 2 ⇔ 40t = 20 + 80(t – 2) ⇒ t = 3,5 h
Vậy ô tô đuổi kịp xe máy sau 3,5 h
Thời điểm ô tô đuổi kịp xe máy là lúc: 6 h + 3,5 h = 9,5 h
Vị trí ô tô đuổi kịp xe máy là x M = 40.3,5 = 140 km

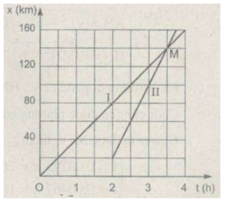
Đồ thị tọa độ của xe máy (đường I) và ô tô (đường II) được vẽ ở trên hình

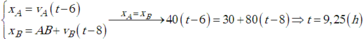



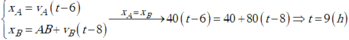
Tóm tắt
\(S_{AB}=20km\)
\(V_1=40km\)/\(h;V_2=80km\)/\(h\)
\(t'=6h;t''=8h\)
______________________
a) \(t=?\)
b) \(S_{AC}=?\)
Giải
a) Gọi \(t_1;t_2\) lần lượt là thời gian đi với vận tốc 40 km/h và 80 km/h.
Ta có: \(S_{AC}-S_{BC}=S_{AB}=20km\Rightarrow V_1.t_1-V_2.t_2=20\)
Trong đó: \(t_1=t_2+2;t_2=t\)
\(\Rightarrow20=40.\left(t+2\right)-80t\Rightarrow20=40t+80-80t\Rightarrow80-20=80t-40t\)
\(\Rightarrow60=40t\Rightarrow t=1,5\left(h\right)\)
b) \(\Rightarrow S_{AC}=40.\left(2+1,5\right)=140\left(km\right)\)
Vậy điểm 2 người gặp nhau cách điểm A là 140km
140km