Trong hiện tượng giao thoa sóng nước 2 nguồn dđ theo phương vuông góc với mặt nước , cùng biên độ, cùng pha, cùng f=50Hz được đặt tại 2 điểm s1, s2 cách nhau 10cm . tốc độ truyền sóng trên mặt nước là 75cm/s . xét các điểm thuộc đường tròn tâm s1 bán kính s1s2 , điểm mà phần tử tại đó dao động với biên độ cực đại cách điểm s2 1 đoạn ngắn nhất bằng ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
26 tháng 6 2018
Đáp án: C
HD Giải: 
M gần S2 nhất nên M nằm trên đường cực đại số 6
Ta có MA - MB = 6λ
=> MB = MA - 6λ
= 10 - 6.1,5 = 1cm = 10mm
VT
1 tháng 10 2018
Đáp án B
Bước sóng :
Trên
S
1
S
2
có 13 điểm dao động với biên độ cực đại 
Cực đại gần S 2 nhất ứng với k = 6
Xét điểm M trên đường tròn
VT
11 tháng 8 2017
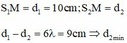
Đáp án C
Bước sóng : λ = v f = 75 50 = 1 , 5 cm
Trên S 1 S 2 có 13 điểm dao động với biên độ cực đại - 6 ≤ k ≤ 6
Cực đại gần S2 nhất ứng với k = 6
Xét điểm M trên đường tròn : S1M = d1 = 10cm; S2M = d2
d 1 - d 2 = 6 λ = 9 cm ⇒ d 2 min = 10 - 9 = 1 cm = 10 mm .
VT
19 tháng 5 2018
- Bước sóng:
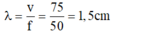
- Trên S1S2 có 13 điểm dao động với biên độ cực đại: -6 ≤ k ≤ 6.
- Cực đại gần S2 nhất ứng với k = 6
- Xét điểm M trên đường tròn :
VT
3 tháng 1 2019
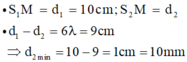
Đáp án A
Bước sóng: λ = v.T = v/f = 80/40 = 2cm
=> Khoảng cách ngắn nhất giữa hai điểm cực đại giao thoa trên đoạn thẳng S 1 S 2 là λ/2 = 1cm
VT
6 tháng 4 2019
Đáp án A
Bước sóng: λ = v.T = v/f = 80/40 = 2cm
=> Khoảng cách ngắn nhất giữa hai điểm cực đại giao thoa trên đoạn thẳng S1S2 là λ/2 = 1cm
.