Question

[Hòa Phạm]

Nối hai cực của một máy phát điện xoay chiều một pha vào 2 đầu đoạn mạch A,B mắc nối tiếp gồm hai điện trở 69,1 Ω, cuộn dây có độ tự cảm L, và tụ điện có điện dung 176,8μF. Bỏ qua điện trở thuần của các cuộn dây của máy phát. Biết roto máy phát có hai cặp cực. Khi roto quay đều với tốc độ n1= 1350 vòng/phút hoặc n2= 1800 vòng/ phút thì công suất tiêu thụ của đoạn mạch AB là như nhau. Độ tự cảm L có giá trị gần giá trị nào nhất:

A.0,7 H

B.0,8 H

C.0,6 H

D.0,2 H

Answer 1

[Nguyen Trung Hau]

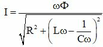
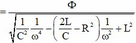
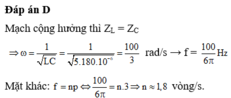
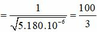
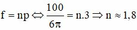
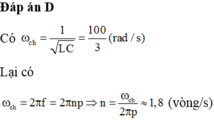
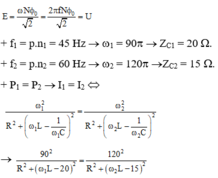
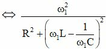
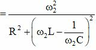
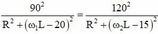
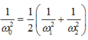
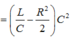
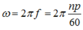
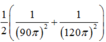
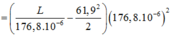
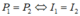
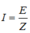
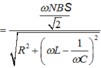
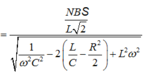
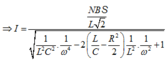
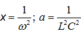
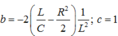
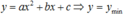
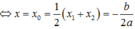
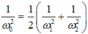
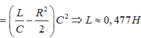
f₁=\(\frac{n_1}{60}\).2=45HZ    ω₁=2πf₁=90π(rad/s)

f₂=\(\frac{n_2}{60}\).2=60HZ    ω₂=2πf₂=120π(rad/s)

P₁=P₂ 

\(\frac{U}{\sqrt{R^2+\left(Z_{L1}-Z_{C1}\right)^2}}=\frac{\frac{4}{3}U}{\sqrt{R^2+\left(Z_{L2}-Z_{C2}\right)^2}}\) thay so tim duoc L=0,477    Dap an:C

Answer 2

[Hoang Hung Quan]

Giải:

\(I=\dfrac{U}{Z}=\dfrac{E}{Z}\) với \(E\) là suất điện động hiệu dụng giữa hai cực máy phát:

\(E=\sqrt{2}\omega N\Phi_0=\sqrt{2}2\pi fN\Phi_0=U\left(r=0\right)\)

Với \(f=np:\) \(n\) tốc độ quay của roto, \(p\) số cặp cực từ

\(\Rightarrow f_1=\dfrac{1350.2}{60}=\dfrac{135}{3}Hz\) \(\Rightarrow\omega_1=90\pi;Z_{C1}=20\Omega\)

\(\Rightarrow f_2=\dfrac{1800.2}{60}=60Hz\) \(\Rightarrow\omega_2=120\pi;Z_{C2}=15\Omega\)

\(P_1=P_2\Leftrightarrow I_1=I_2\)

\(\Leftrightarrow\dfrac{\omega_1^2}{R^2+\left(\omega_1L-\dfrac{1}{\omega_1C}\right)^2}=\) \(\dfrac{\omega_2^2}{R^2+\left(\omega_2L-\dfrac{1}{\omega_2C}\right)^2}\)

\(\Rightarrow\dfrac{90^2}{R^2+\left(\omega_1L-20\right)^2}=\dfrac{120^2}{R^2+\left(\omega_2L-15\right)^2}\)

\(\Rightarrow\dfrac{9}{R^2+\left(\omega_1L-20\right)^2}=\dfrac{16}{R^2+\left(\omega_2L-15\right)^2}\)

\(\Leftrightarrow9\left[R^2+\left(\omega_2L-15\right)^2\right]\) \(=16\left[R^2+\left(\omega_1L-20\right)^2\right]\)

\(\Leftrightarrow-7R^2+\left(9\omega_2^2-16\omega_1^2\right)L^2-\) \(\left(270\omega_2-640\omega_1\right)L\) \(+9.15^2-16.20^2=0\)

\(\Leftrightarrow\left(9\omega_2^2-16\omega_1^2\right)L^2-\left(270\omega_2-640\omega_1\right)L\) \(-7R^2+9.15^2\)\(-16.20^2=0\)

\(\Leftrightarrow25200\pi L=37798,67\Rightarrow L=0,48H\)

Vậy ta chọn đáp án \(C\)