Cho trước n điểm ( n ∈ N; n ≥ 2). Vẽ các đoạn thẳng đi qua các cặp điểm được tất cả 28 đoạn thẳng. Tìm n.
HELP ME PLEASE ~ ! 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 5 2019
a) Nếu trong 7 điểm đã cho không có ba điểm nào thẳng hàng thì số đường thẳng vẽ được A 7 . 7 − 1 2 = 21 (đường thẳng).
Xét ba điểm thẳng hàng, qua chúng chỉ vẽ được một đường thẳng. Nếu ba điểm này không thẳng hàng thì vẽ được ba đường thẳng.
Số đường thẳng giảm đi là: 3 – 1 = 2 (đường thẳng)
Vậy vẽ được tất cả 21 – 2 = 19 (đường thẳng).
b) Lập luận tương tự như câu a), qua 12 điểm trong đó có đúng ba điểm thẳng hàng ta vẽ được 12 . 12 − 1 2 − 2 = 64 (đường thẳng)
c) Lập luận tương tự như câu a), qua n điểm trong đó có đúng ba điểm thẳng hàng ta vẽ được n . n − 1 2 − 2 (đường thẳng)
CM
1 tháng 11 2019
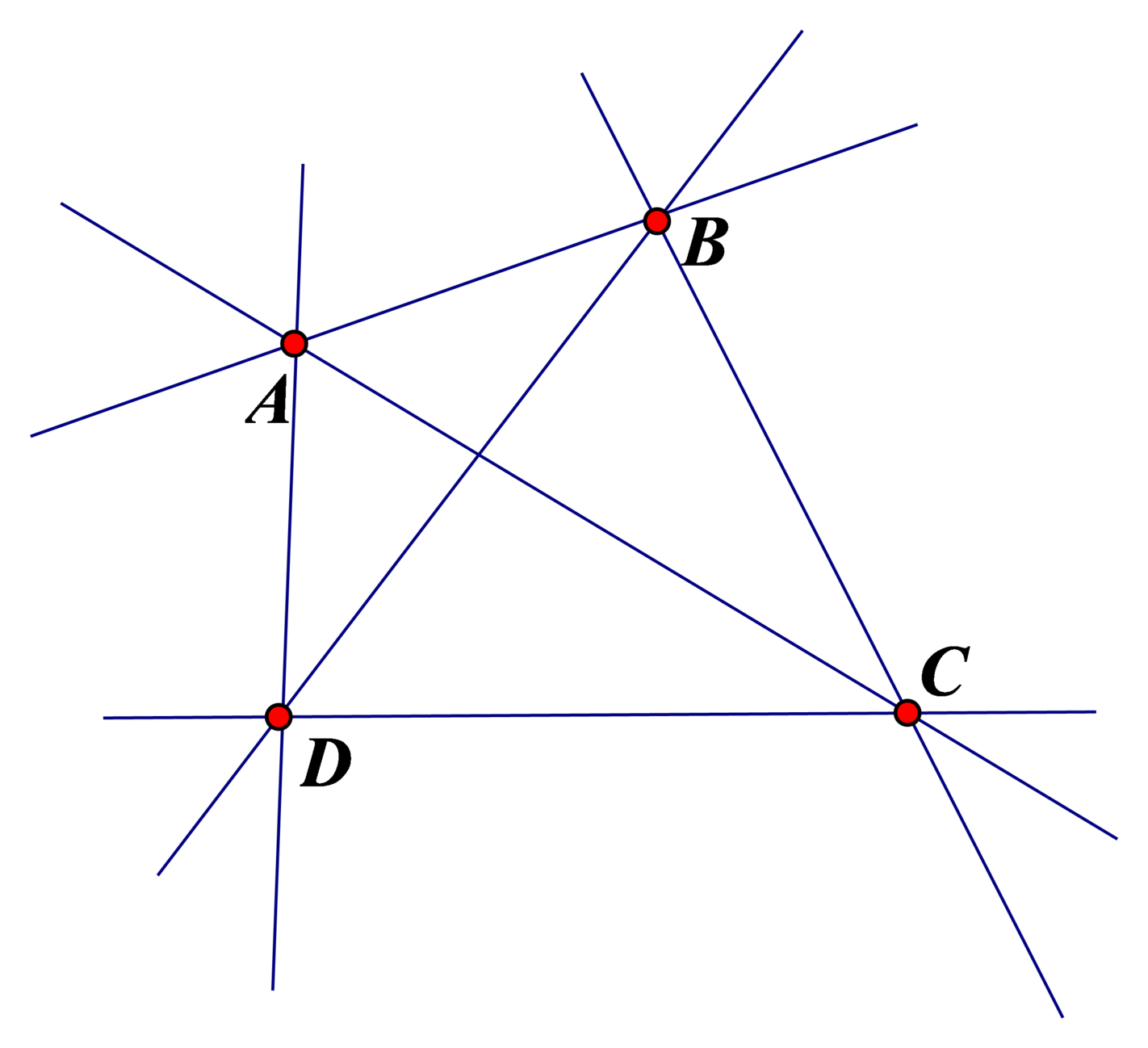
a) Với 4 điểm A, B, C, D cho trước trong đó không có ba điểm bất kì nào thẳng hàng thì có thể vẽ được 6 đường thẳng là: AB , AC , AD , BC , BD , CD .
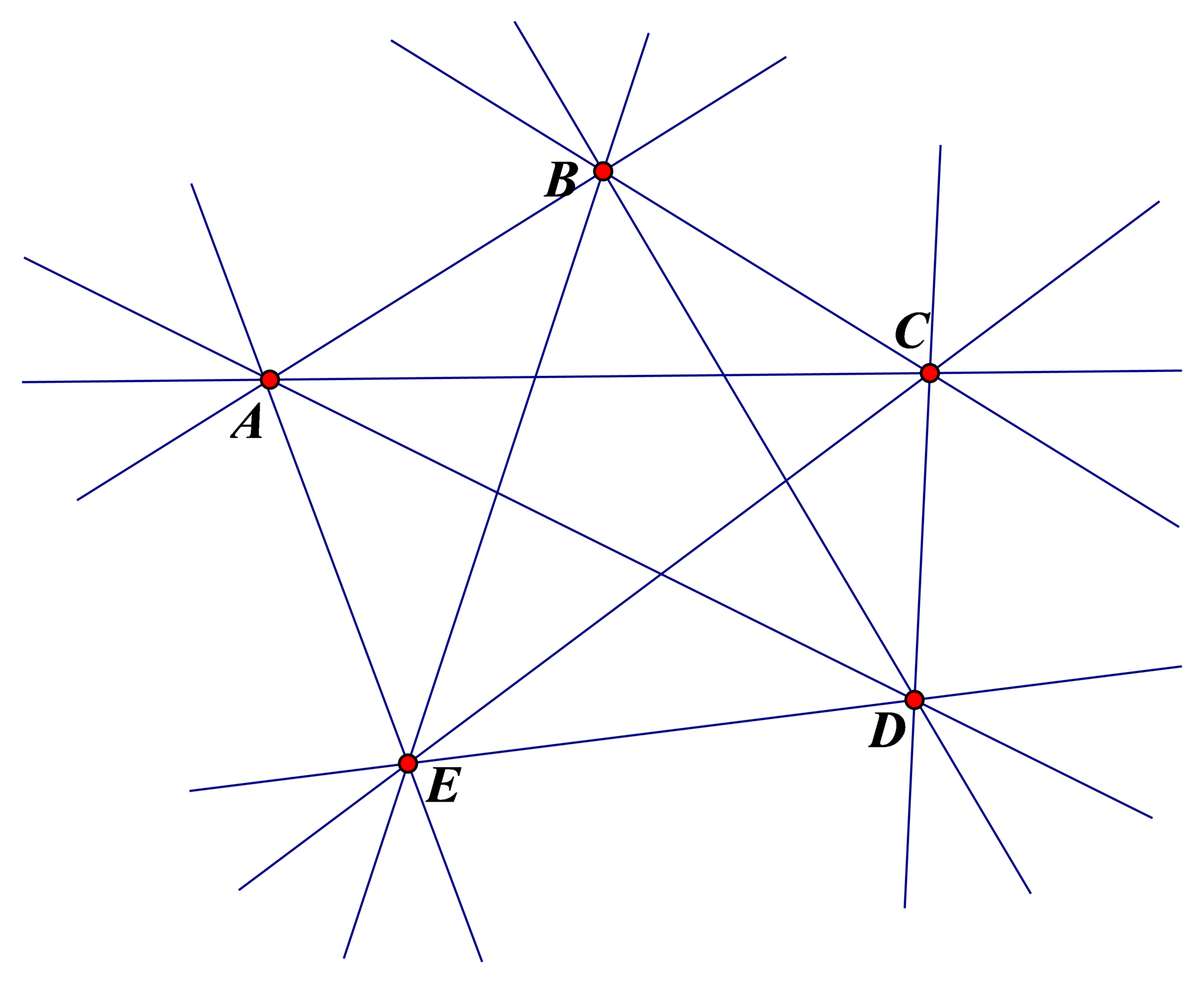
b) Với 5 điểm A, B, C, D, E cho trước trong đó không có ba điểm bất kì nào thẳng hàng thì có thể vẽ được 10 đường thẳng là: AB , AC , AD , AE , BC , BD , BE , CD , CE , DE .
c) Chọn một trong số n điểm đã cho rồi nối điểm đó với n-1 điểm còn lại ta được n-1 đường thẳng.
Làm như vậy với tất cả n điểm ta được n(n-1) đường thẳng. Nhưng mỗi đường thẳng được tính hai lần, do đó ta vẽ được n . n − 1 2 đường thẳng.
Vì số đoạn thẳng được lặp đi lặp lại 2 lần.
\(\Rightarrow\) Số đoạn thẳng nếu không được lặp lại là:
28 . 2 = 56 (đoạn thẳng)
Ta thấy: 56 = (n-1) . n = 7 . 8
\(\Rightarrow\) n - 1 = 7 và n = 8
Vậy n = 8.