giúp mình với:
phân tích đa thức sau thành nhân tử;
3x3-14x2+4x+3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^5-1=\left(x-1\right)\left(x^4+x^3+x^2+x+1\right)\)
- Đúng thì k hộ tớ nhé ^^

= \(5x^3-2x^2-10x^2+4x+10x-4\)
= \(5x^2\left(x-\frac{2}{5}\right)-10x\left(x-\frac{2}{5}\right)+10\left(x-\frac{2}{5}\right)\)
=\(\left(x-\frac{2}{5}\right)\left(5x^2-10x+10\right)\)
Chuc ban hoc tot!

Áp dụng hằng đẳng thức hiệu 2 bình phương .
\(4x^2-3y^2\)
\(=\left(2x\right)^2-3y^2\)
\(=\left(2x+3y\right)\left(2x-3y\right)\).
_ Chúc bạn học tốt _

`n)x^2+4x+3`
`=x^2+3x+x+3`
`=x(x+3)+(x+3)`
`=(x+3)(x+1)`
`b)x^2+6x+8`
`=x^2+4x+2x+8`
`=x(x+4)+2(x+4)`
`=(x+4)(x+2)`
`->` tách ra nha bạn
\(10,\\ a,x^2-6x+5\\ =x^2-x-5x+5\\ =x\left(x-1\right)-5\left(x-1\right)\\ =\left(x-1\right)\left(x-5\right)\)
\(b,x^2+6x+8\\ =x^2+4x+2x+8\\ =x\left(x+4\right)+2\left(x+4\right)\\ =\left(x+4\right)\left(x+2\right)\)
\(c,2x^2+10x+8\\ =2\left(x^2+5x+4\right)\)
\(d,x^2-5x+14\)
`->` Có đúng đề không cậu nhỉ ?
\(e,x^2-7x+10\\ =x^2-2x-5x+10\\ =x\left(x-2\right)-5\left(x-2\right)\\ =\left(x-2\right)\left(x-5\right)\)
\(g,3x^2-5x-2\\ =3x^2+x-6x-2\\ =x\left(3x+1\right)-2\left(3x+1\right)\\ =\left(3x+1\right)\left(x-2\right)\)
\(h,2x^2+x-6\\ =2x^2+4x-3x-6\\ =2x\left(x+2\right)-3\left(x+2\right)\\ =\left(x+2\right)\left(2x-3\right)\)
\(i,x^2-9x+18\\ =x^2-3x-6x+18\\ =x\left(x-3\right)-6\left(x-3\right)\\ =\left(x-3\right)\left(x-6\right)\)
\(k,2x^2-6x+9\)
`->` Cậu xem lại đề
\(e,3x^2-5x-2\\=3x^2+x-6x-2\\ =x\left(3x+1\right)-2\left(3x+1\right)\\ =\left(3x+1\right)\left(x-2\right)\)
`m,` \(x^2-5+6\)
`->` Cậu xem lại đề

Đề sai nhé .Sửu lại
\(x^2-4x^2y^2+4+4x\)
\(=\left(x^2+4x+4\right)-4x^2y^2\)
\(=\left(x+2\right)^2-\left(2xy\right)^2\)
\(=\left(x+2+2xy\right)\left(x+2-2xy\right)\)


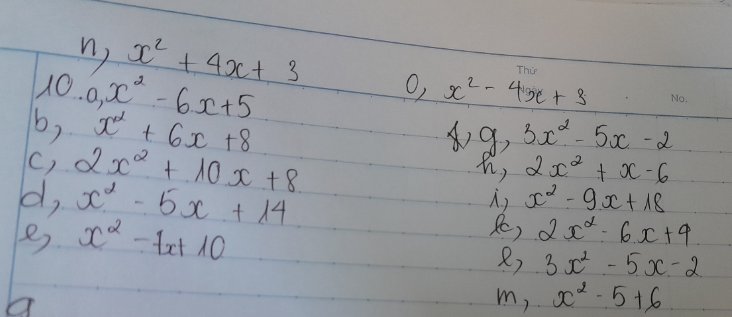
\(A=3x^2-14x^2+4x+3\)
Giả sử:
\(A=\left(3x+a\right)\left(x^2+bx+c\right)\)
\(=3x^3+3bx^2+3cx+ax^{2\:}+abx+ac\)
\(=3x^3+\left(3b+a\right)x^2+\left(3c+ab\right)x+ac\)
Ta có:
\(\begin{cases}3b+a=-14\\3c+ab=4\\ac=3\end{cases}\)\(\Rightarrow\begin{cases}a=1\\b=-5\\c=3\end{cases}\)
Vậy \(A=\left(3x+1\right)\left(x^2-5x+3\right)\)