Một vật nhỏ có khối lượng m=400g được treo vào một lò xo khối lượng không đáng kể, độ cứng k=40N/m. Đưa vật lên đến vị trí lò xo không bị biến dạng rồi thả nhẹ cho vật dao động. Cho g= 10m/s2. Chọn gốc tọa độ tại vị trí cân bằng, chiều dương hướng xuống dưới và gốc thời gian khi vật ở vật ở vị trí lò xo bị giãn một đoạn 5cm và vật đang đi lên. Bỏ qua mọi lực cản. Phương trình dao động của vật sẽ là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vị trí lực đàn hồi cân bằng với trọng lực:
kx0 = mg => x0 = 0,02 m = 2 cm.
b) Vận tốc của vật tại vị trí lực đàn hồi cân bằng với trọng lực:
1/2 . k(xo)2 = ½k(vcb)2 => |vcb| = 0,2√5 m/s = 20√5 (cm/s).
a. Ở vị trí cân bằng thì lực đàn hồi cân bằng với trọng lượng
\(\Rightarrow F_{đh}=P\Rightarrow k.\Delta l_0=mg\)
\(\Rightarrow \Delta l_0=\dfrac{mg}{k}=\dfrac{0,4.10}{200}=0,02m=2cm\)
b. Vị trí đó chính là vị trí cân bằng.
Chọn gốc thế năng ở vị trí cân bằng.
Thả vật ở vị trí lò xo không giãn \(\Rightarrow x_1=2cm\)
Áp dụng định luật bảo toàn cơ năng ta có:
\(\dfrac{1}{2}.k.x_1^2=\dfrac{1}{2}.m.v^2\)
\(\Rightarrow v = x_1.\sqrt{\dfrac{k}{m}}=2.\sqrt{\dfrac{200}{0,4}}==20\sqrt 5 (cm/s)\)

Ta có:\(\Delta\)l=4cm;A=8cm;T=2\(\pi\)\(\sqrt{\frac{\Delta l}{g}}\)=0,4(s)
2\(\alpha\)=\(\omega\)\(\Delta\)t nén
\(\Rightarrow\)\(\Delta\)t nén =\(\frac{2\alpha}{\omega}\)=\(\frac{2arccos\frac{\Delta l}{A}}{\frac{2\pi}{T}}\)=\(\frac{2.\frac{\pi}{3}}{2\pi}\).o,4=\(\frac{2}{15}\)(s)
Có j sai sót mong mn giúp đỡ![]()

Chọn C.
Khi buộc đầu dưới vật khối lượng m1, lò xo dãn:
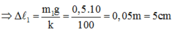
Khi buộc vào điểm giữa của lò xo một vật nặng thứ hai, thì nửa trên của lò xo có độ cứng k’. Vì độ cứng k của lò xo tỷ lệ nghịch với chiều dài ℓ nên
![]()
Khi buộc vào chính giữa lò xo vật m2 nửa trên dãn thêm:
![]()
⟹ Chiều dài lò xo lúc này là:
![]()

Chọn C.
Khi buộc đầu dưới vật khối lượng m 1 , lò xo dãn:
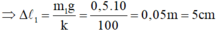
Khi buộc vào điểm giữa của lò xo một vật nặng thứ hai, thì nửa trên của lò xo có độ cứng k’. Vì độ cứng k của lò xo tỷ lệ nghịch với chiều dài ℓ nên
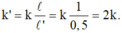
Khi buộc vào chính giữa lò xo vật m 2 nửa trên dãn thêm:
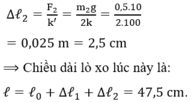




Biên độ: \(A=10cm\)
Tần số góc: \(\omega=10(rad/s)\)
Tại vị trí lò xo bị giãn \(5cm\) thì li độ của vật là: \(x=-10+5=-5cm\)
Vật đang đi lên là chuyển động theo chiều âm.
\(\Rightarrow \cos\varphi=-\dfrac{5}{10}=-0,5\)
\(\Rightarrow \varphi = \dfrac{2\pi}{3}\) (rad) (vì vật chuyển động theo chiều âm nên \(\varphi < 0\) )
PT dao động: \(x=10\cos(10t+\dfrac{2\pi}{3}) (cm)\)
Ở VTCB lò xo giãn 10 cm, như vậy để nó giãn 5cm thì từ VTCB phải đi lên 5cm.
Chiều dương hướng xuống, nên li độ lúc đó phải bằng -5cm.