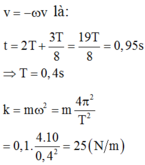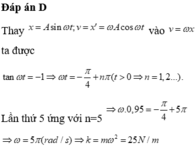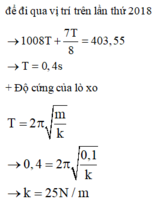Một con lắc lò xo dao động điều hòa theo phương ngang với tần số góc . Vật nhỏ của con lắc có khối lượng 100 g. Tại thời điểm t = 0, vật nhỏ qua vị trí cân bằng theo chiều dương. Tại thời điểm t = 24173/60 s, vận tốc v và li độ x của vật thỏa mãn \(v=\left(2-\sqrt{3}\right)\omega x\) lần thứ 2015. Lấy \(\pi^2=10\). Độ cứng của lò xo là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tại t = 0,95s, v = - ω x ⇒ A ω cos ω t = - ω A cos ω t - π 2 ⇔ tan ω t = - 1 ⇔ ω t = - π 4 + k π
Vì ωt > 0 và k nguyên nên suy ra k phải nguyên dương. Khi k = 1 thì vật sẽ đạt v = -ωx lần thứ nhất…, suy ra khi k = 5 vật sẽ đạt trạng thái này lần thứ 5.
Ta có 0 ٫ 95 ω = - π 4 + 5 π ⇔ ω = 5 π rad / s ⇒ k = ω 2 m = 25 N / m

Đáp án D
Ta có ![]()
Khi 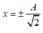 ta có
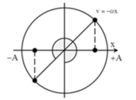
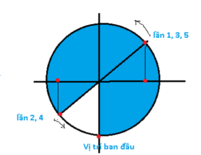
ta có ![]() khi pha dao động của vật trên đường tròn đơn vị là π/4 hoặc 3π/4 rad. (Mỗi chu kì có 2 lần vận tốc của vật v = -ωx).
khi pha dao động của vật trên đường tròn đơn vị là π/4 hoặc 3π/4 rad. (Mỗi chu kì có 2 lần vận tốc của vật v = -ωx).
Tại t = 0 vật qua VTCB theo chiều dương → pha ban đầu là –π/2 rad.
Ta có 7 = 3.2 + 1 → t = 0,825 = 3T + 3T/8 = 27T/8
→ T = 0,24 s → k = 69 N/m.

Đáp án D
Tại thời điểm t = 0,95 s, vận tốc của vật:
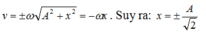
Trong một chu kì vật đi qua vị trí có v = - ω x hai lần. Lần thứ 5 vật đi qua vị trí thỏa mãn hệ thức đó là
![]()
Độ cứng của lò xo: k = 25 N/m

Đáp án D.
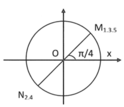
- Thời điểm vận tốc v và li độ x của vật nhỏ thỏa mãn
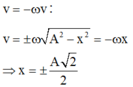
Trong một chu kì, vật qua vị trí có li độ thỏa v = - ω v hai lần. Tại thời điểm ban đầu vật qua vị trí cân bằng theo chiều dương (vị trí M 0 ) nên lần thứ 5 vật qua vị trí có li độ thỏa