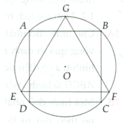
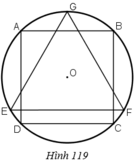
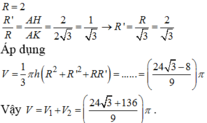Cho tam giác đều và hình vuông cùng nội tiếp một hình tròn sao cho một cạnh của tam giác đều song song với một cạnh của hình vuông. Lập công thức tính diện tích phần giao nhau giữa tam giác đều và hình vuông khi biết bán kính r của đường tròn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 5 2018
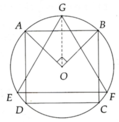
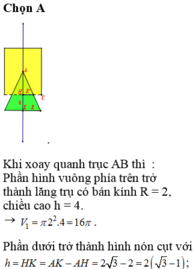
a, V h t A B C D = π AB 2 2 . BC = π AB 3 4 = π 2 2 . R 3 (1)
V h c = 4 3 πR 3 (2)
V h n = 1 3 π EF 2 2 . GH = 1 8 3 π . EF 3 . Tính được GO = 3 R
=> V h n = 1 8 3 π 3 3 R 3 = 3 8 πR 3 (3)
Từ (1), (2) và (3) => ĐPCM
b, S t p h t = 3 πR 2 (4); S h c = 4 πR 2 (5)
S t p h n = 3 4 πEF 2 = 3 4 π . 3 R 2 = 9 4 πR 2 (6)
Từ (4); (5) và (6) => ĐPCM
CM
26 tháng 6 2019
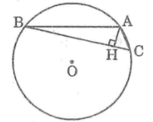
Dây AB bằng cạnh hình vuông nội tiếp đường tròn (O) nên ta có: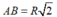 
và cung nhỏ AB có số đo bằng
360
°
:
4
=
90
°
Dây BC bằng cạnh hình tam giác đều nội tiếp đường tròn (O) nên ta có:
BC = R 3 và cung nhỏ BC có số đo bằng 360 ° : 3 = 120 °
Ta có:
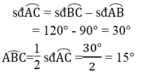
Trong tam giác vuông ABH ta có:
Trong tam giác vuông ACH ta có:
20 tháng 1 2018
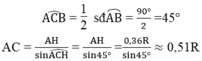
Gọi độ dài cạnh hình vuông là a , độ dài cạnh tam giác là b . Theo bài ra ta có :
4 . a = 3 . b
b - a = 4 cm
Thay vào ta có :
\(4b-16=3b\Rightarrow b=16\left(cm\right)\)
Chu vi tam giá đều là :
16 . 3 = 48 cm
Cạnh hình vuông là :
48 : 4 = 12 cm
Diện tích hình vuông là :
12 . 12 = 144 cm2
