mn cho tui hỏi cái
tìm min max của |f(x)| ý
sao Max lại tìm theo 2TH còn min lại tìm theo so sánh trên dưới với trục ox vậy
tai sao lại không thể làm theo cách của tìm max
dạng mà tìm tham số m để hàm số |f(x)| có Min/Max trên [a,b] ý
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Vì a=-1<0 nên hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (-∞;2]
Bảng biến thiên là:
| x | -∞ | 2 | +∞ |
| y | -∞ | 1 | -∞ |


a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

Chọn A
Hàm số y = f(x) = 2 x + m x - 1 . xác định và liên tục trên [2;3].
Với m = -2, hàm số trở thành y = 2![]() (không thỏa)
(không thỏa)
Với ![]() ta có:
ta có: 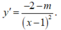
Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]
Suy ra 
Do đó: ![]()
![]()
Theo giả thiết ![]()
![]()
Vậy tổng các giá trị của tham số thỏa mãn yêu cầu bài toán là: -4.
Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức ![]() là không cần thiết.
là không cần thiết.

Chọn A
Hàm số y = f(x) =
2
x
+
m
x
-
1
xác định và liên tục trên [2;3]
Với m = -2, hàm số trở thành y = 2 ![]() (không thỏa).
(không thỏa).
Với m
≠
2, ta có: 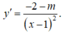
Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]
Suy ra

Do đó:
![]()
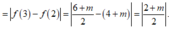
Theo giả thiết
![]()
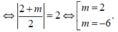
Vậy tổng các giá trị của tham số thỏa mãn yêu cầu bài toán là: -4.
Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức ![]() là không cần thiết.
là không cần thiết.
@Nguyễn Việt Lâm giúp em với ạ