Tìm tất cả các giá trị của m>1 để giá trị lớn nhất của hàm số f(x)=(2.cănx +m)/(căn(x+1)) trên đoạn [0,4] không lớn hơn 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ Đạo hàm f'(x) = 2 - m x 2 ( x + 1 ) x ( x + 1 )
f'(x) = 0 ⇒ x = 2 m ↔ x = m 2 4 ∈ [ 0 ; 4 ] , ∀ m > 1
+ Lập bảng biến thiên, ta kết luận được
m a x [ 0 ; 4 ] f ( x ) = f ( 4 m 2 ) = m 2 + 4
+ Vậy ta cần có m 2 + 4 < 3
↔ m < 5 → m > 1 m ∈ ( 1 ; 5 )
Chọn C.

Chọn A.
TXĐ: D = R.
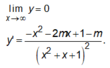
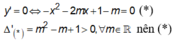 có 2 nghiệm phân biệt
có 2 nghiệm phân biệt ![]()
BBT:
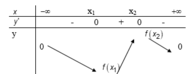
Vậy hàm số đạt giá trị lớn nhất là
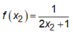
![]()
YCBT 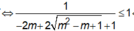
![]()
![]()
![]()
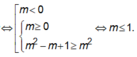

\(y=\left|x^2-2x-m\right|=-x^2+2x+m\)
\(\left(nếu:x^2-2x-m< 0\right)\)
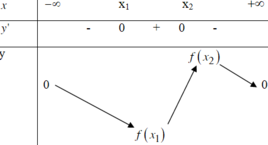
\(f\left(x\right)=-x^2+2x+m\Rightarrow x=\dfrac{-b}{2a}=1\in\left[-3;2\right]\)
\(f\left(-3\right)=m-15\)
\(f\left(1\right)=m+1\)
\(f\left(2\right)=m\Rightarrow f\left(-3\right)< f\left(2\right)< f\left(1\right)\)
\(\Rightarrow max_{f\left(x\right)}=m+1=10\Leftrightarrow m=9\)
\(do..m< 0\Rightarrow m=9\left(ktm\right)\)
\(\Rightarrow không\) \(có\) \(giá\) \(trị\) \(m\) \(thỏa\)

Đạo hàm f'(x) = m 2 - m + 1 ( x + 1 ) 2 > 0, ∀ x ∈ [ 0 ; 1 ]
Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m2+m
Theo bài ta có:
-m2+ m= -2 nên m= -1 hoặc m= 2.
Chọn D.
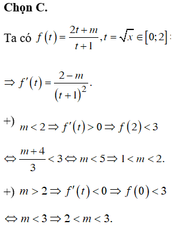

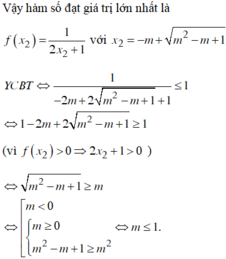
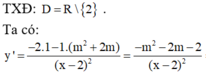
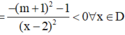
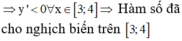
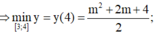
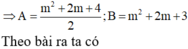

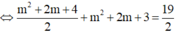
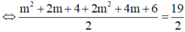
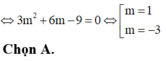
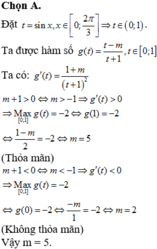
\(f'\left(x\right)=\frac{\frac{\sqrt{x+1}}{\sqrt{x}}-\frac{\sqrt{x}}{\sqrt{x+1}}}{x+1}=\frac{1}{\sqrt{x}\left(\sqrt{x+1}\right)^3}>0;\forall x\in\left(0;4\right)\)
Mà f(x) liên tục trên [0;4] nên hàm số đồng biến trên [0;4]
\(\Rightarrow Maxf\left(x\right)_{\left[0;4\right]}=f\left(4\right)\)
YCBT \(\Leftrightarrow\begin{cases}m>1\\f\left(4\right)\le3\end{cases}\) \(\Leftrightarrow\begin{cases}m>1\\\frac{4+m}{\sqrt{5}}\le3\end{cases}\)\(\Leftrightarrow1< m< 3\sqrt{5}-4\)