Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét ΔBDC có
M là trung điểm của BC
E là trung điểm của DB
Do đó: ME là đường trung bình của ΔBDC
Suy ra: ME//DC
Xét ΔAME có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM
hay AI=IM
a)Áp dụng định lí pytago vào tam giác ABC vuông tại A, ta có
BC^2=AB^2+AC^2
=>BC^2=4^2+3^2
=>BC^2=16+9=25
=>BC=căn25=5 (cm)
vậy,BC=5cm
b)Xét tam giác ABC và AED có
AB=AE(gt)
 là góc chung
AC=AD(gt)
=>tam giác ABC=tam giác AED(c-g-c)
Xét tam giác AEB có:Â=90*;AE=AB
=>tam giác AEB vuông cân tại A
Vậy tam giác AEB vuông cân
c)Ta có EÂM+BÂM=90*
mà BÂM+MÂB=90*
=>EÂM=MÂB
mà MÂB=AÊD(cm câu b)
=>EÂM=AÊD hay EÂM=AÊM
xét tam giác EAM có: EÂM=AÊM(cmt)
=>tam giác EAM cân tại M
=>ME=MA (1)
Ta có góc ACM+CÂM=90*
mà BÂM+CÂM=90*
=>góc ACM=BÂM
mà góc ACM=góc ADM( cm câu b)
=>góc ADM=DÂM
Xét tam giác MAD có góc ADM=DÂM(cmt)
=>tam giác ADM cân tại M
=>MA=MD (2)
Từ (1) và (2) suy ra MA=ME=MD
ta có định lí:trong 1 tam gáic vuông, đg trung truyến ứng với cạnh huyền bằng nửa cạnh huyền
=>MA=1/2ED
=>MA là đg trung tuyến ứng với cạnh ED
Vậy MA là đg trung tuyến của tam giác ADE
a,Ta có :
DM // BC , EN // BC ⇒ DM // EN
Vì AD = DE và DM // EN
⇒⇒ DM là đường trung bình của tam giác AEN
⇒AM=MN (1)
⇒M là trung điểm của AN
2b, Xét hình thang DMCB
DE=EB và EN // BC
⇒ EN là đường trung bình của hình thang DMCD
⇒MN=NC (2)
Từ (1) và (2) ⇒AM=MN=NC
a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI
Xét ΔBDC có
M là trung điểm của BC
E là trung điểm của BD
Do đó: ME là đường trung bình của ΔBDC
Suy ra: ME//DK
Xét ΔAEM có
D là trung điểm của AE
DK//EM
Do đó: K là trung điểm của AM
hay KA=KM
a: Xét ΔBDC có
E là trung điểm của BD
M là trung điểm của BC
Do đó: EM là đường trung bình của ΔBDC
Suy ra: EM//DC
b: Xét ΔAME có
E là trung điểm của AD
DI//EM
Do đó: I là trung điểm của AM
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
b: AM=ED/2
AN=BC/2
mà ED=BC
nên AM=AN
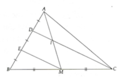
a)Ta có \(\begin{cases}BE=ED=\frac{1}{2}BD\\BM=MC\end{cases}\) => ME là đường trung bình của tam giác BDC
=> EM // CD => EMCD là hình thang.
b) Ta chứng minh được ME // CD hay ME // ID (câu a) =>DIME là hình thang
Lại có AD = DE => DI là đường trung bình của tam giác AEM => AI = IM => I là trung điểm AM