Trên một đoạn đường thẳng AC có điểm B nằm giữa sao cho BC = 4.AB. Tại thời điểm t0 = 0, xe thứ nhất chuyển động đều qua A với tốc độ v1 hướng về C, xe thứ hai chuyển động đều qua B với tốc độ v2 cùng hướng với xe thứ nhất. Đến thời điểm t = 1,5 h, hai xe gặp nhau tại C. Biết rằng quãng đường mỗi xe đi được trong một giờ hơn kém nhau 10 km. Tính v1, v2 và độ dài quãng đường AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, khi cd ngược chiều
\(\dfrac{S}{v_1+v_2}=50\left(1\right)\)
khi cđ cùng chiều
\(\dfrac{S}{v_1-v_2}=350\left(s\right)\left(2\right)\)
từ (1) và (2) => v1=8m/s v2=6m/s
b, vuông góc nên có pitago nhá
gọi x là khoảng cách gần nhất D là vị trí xe 2 lúc đó C là vị trí xe 1 ta có
\(x^2=CB^2+BD^2\)
\(x^2=\left(AB-AC\right)^2+BD^2\)
\(x^2=\left(700-8t\right)^2+\left(6t\right)^2\)
\(\Leftrightarrow x^2=100t^2-11200t+490000=\left(10t-560\right)^2+176400\)
\(\Rightarrow x^2_{min}\Leftrightarrow\left(10t-560\right)^2=0\Rightarrow t=56s\)
\(\Rightarrow x=\sqrt{176400}=420\left(m\right)\)

Đáp án B
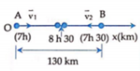
Chọn trục Ox trùng với đường AB, gốc O tại A, chiều dương hướng từ A sang B. Gốc thời gian là lúc 7 giờ . Sau thời gian t >0,5h;
- Toạ độ của xe thứ nhất: ![]()
- Toạ độ của xe thứ hai: ![]()
Khi hai xe gặp nhau lúc 8 giờ 30 phút hay t=1,5h
![]()
(Dễ thấy với t <0,5h xe thứ nhất không thể gặp xe thứ hai)


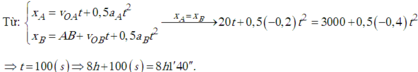
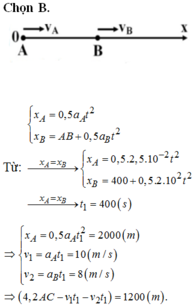
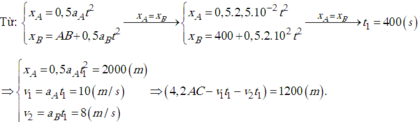
quãng đường mỗi xe đi trong 1h chênh nhau 10km nên \(v_1-10=v_2\left(1\right)\)
quãng đường xe 1 đi đến C \(v_1.1,5=AC\left(2\right)\)
quãng đường xe 2 đi đến C \(v_2.1,5=BC\) \(\Rightarrow v_2.1,5+AB=AC\) mà AB=1/5AC vì BC+AB=AC mà BC=4AB
\(\Rightarrow v_2.1,5+\dfrac{1}{5}AC=AC\Rightarrow v_2.1,5=\dfrac{4}{5}AC\left(3\right)\)
chia 2 vế 2 3 cho nhau \(\dfrac{v_1}{v_2}=\dfrac{1}{\dfrac{4}{5}}\) kết hợp vs (1) \(\dfrac{v_1}{v_1-10}=\dfrac{1}{\dfrac{4}{5}}\Rightarrow v_1=50\left(km/h\right)\)
=> v2=40(km/h)
=>AC=50.1,5=75(km)