Một phân thức có dạng \(\frac{k^2-5k+8}{k^2+6k+19}\) với \(k\in N\). Chứng Minh rằng nếu tử thức (hoặc mẫu thức) chia hết cho 11 thì mẫu thức (hoặc tử thức) chia hết cho 11.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 10 2017
Thật vậy, ta có:
x3 + 5x2 – 4x – 20
= x3 + 3x2 – 10x + 2x2 + 6x – 20
= x(x2 + 3x – 10) + 2(x2 + 3x – 10)
= (x + 2)(x2 + 3x – 10)
⇒ x3 + 5x2 – 4x – 20 chia hết cho x2 + 3x – 10
x3 + 5x2 – 4x – 20
= x3 + 7x2 + 10x – 2x2 – 14x – 20
= x(x2 + 7x + 10) – 2.(x2 + 7x + 10)
= (x – 2)(x2 + 7x + 10)
⇒ x3 + 5x2 – 4x – 20 chia hết cho x2 + 7x + 10
Do đó có thể chọn mẫu thức chung là x3 + 5x2 – 4x – 20.
CM
2 tháng 2 2017
Gợi ý: M = ( a 2 – a – 2)(a + 2) = ( a 2 + 3a + 2)(a – 2).
Do đó, ta có thể quy đồng mẫu thức của hai phân thứ này với mẫu thức chung là M = a 3 + a 2 – 4a – 4.
AH
Akai Haruma
Giáo viên
10 tháng 1 2017
Lời giải:
Ta có các điều sau:
\(\left\{\begin{matrix} a+b\equiv 0\pmod k\\ c+d\equiv 0\pmod k\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a\equiv -b\pmod k\\ d\equiv-c\pmod k\end{matrix}\right.\)
Áp dụng tính chất nhân của mo- đun:
\(\Rightarrow ad\equiv (-b)(-d)=bd\pmod k\) . Suy ra $ad-bc$ chia hết cho $k$
Do đó ta có đpcm
9 tháng 8 2016
9a + b + 4c = 3(3a + 4b + 5c) - 11(b + c) = 3*11*N - 11(b + c) = 11*(3*N - b - c) chia hết cho 11
9 tháng 8 2016
9a+b+4c=3(3a+4b+5c)-11(b+c=3*11*N-11(b-c)=11*(3*N-b-c) chia het co 11
lam dung k minh ngay nhe
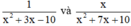
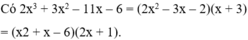
Chứng minh tử thức (hoặc mẫu thức) chia hết cho 11 thì mẫu thức (hoặc tử thức) chia hết cho 11 nghĩa là ta chứng minh nếu \(k^2-5k+8\)chia hết cho 11 thì \(k^2+6k+9\)cũng chia hết cho 11 và ngược lại.
Ta có :
\(k^2-5k+8\)chia hết cho 11
Mà \(11k\)chia hết cho 11
\(11\)chia hết cho 11
\(\Rightarrow k^2-5k+8+11k+11\)chia hết cho 11
\(\Rightarrow k^2+6k+19\)chia hết cho 11
Chứng minh ngược lại :
\(k^2+6k+19\)chia hết cho 11
Mà \(11k;11\)chia hết cho 11
\(\Rightarrow k^2+6k+19-11k-11\)chia hết cho 11
\(\Rightarrow k^2-5k+8\)chia hết cho 11
Vậy ...