1) Một Cây tre cao 9m , bị gẫy ngang thân , ngọn cây chạm đất cách góc 3m . Hỏi điểm gãy cách gốc bao nhiêu ?
2) Cho tam giác ABC , trung tuyến AM cũng là PG
a) Chứng minh rằng tam giác ABC cân
c) Cho hết AB = 37 , AM = 35 . tính BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
25 tháng 4 2018
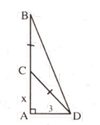
Giả sử AB là độ cao của cây tre, C là điểm gãy.
Đặt AC = x (0 < x < 9) => CB = CD = 9 – x.
Vì ∆ ACD vuông tại A
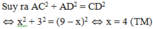
Vậy điểm gãy cách gốc cây 4m
Đáp án cần chọn là: C
NH
Một cây tre cao 9m bị gãy ngang thân, ngọn cây chạm đất cách gốc 3m. Hỏi độ dài từ điểm gãy tới gốc?
1

6 tháng 3 2016
gọi CDài phần còn lại là a (m)
=> phần gãy là 9-a (m)
áp dụng ĐL py-ta-go ta có: a2 + 32 =( 9-a)2
=> a2+9 = (9-a).(9-a)
a2+9 = 81 - 18a +a2
=> 18a = 81-9 = 72=> a= 72:18 = 4 m
vậy điểm gãy cách gốc 4 m
duyệt đi
TH
0

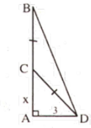

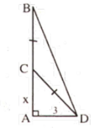

AM là trung tuyến \(\Rightarrow\) M1=M2=90o
vì AM là phân giác\(\Rightarrow\) A1=A2
xét tam giác AMB và AMC
cạnh AM chung
A1=A2
M1=M2=90o
\(\Rightarrow\) AMB=AMC(g.c.g)
\(\rightarrow\) AB=AC(2 cạnh tương ứng)
vậy tam giác ABC cân tại A
b) vì M1 vuông
ta có AB2= AM2+BM2( định lí pi-ta-go)
vì AB=37,AM=35
\(\Rightarrow\) 372= 352+BM2
MB2= 372-352
MB2=144
MB=12 cm
chúc bạn học tốt(like mình nha)
Gọi chiều dài phần còn lại là x(m)
\(\Rightarrow\)Phần gãy là 9-x(m)
Áp dụng định lí Pitago ta có :x2+ 32=(9-x)2
\(\Rightarrow\)x2+9=(9-x)(9-x)
\(\Rightarrow\)x2+9=81-18x+x2
\(\Rightarrow\)18x=81-9=72\(\Rightarrow\)x=72:18=4 m
Vậy điểm gãy cách gốc 4m
Chúc bn học tốt nha!!!!!!!!