\(sin^6\left(x\right)cos^2\left(x\right)+sin^2\left(x\right)cos^6\left(x\right)=\frac{1}{8}\left(1-cos^4\left(2x\right)\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 2 bạn coi lại đề
3.
\(1+2sinx.cosx-2cosx+\sqrt{2}sinx+2cosx\left(1-cosx\right)=0\)
\(\Leftrightarrow sin2x-\left(2cos^2x-1\right)+\sqrt{2}sinx=0\)
\(\Leftrightarrow sin2x-cos2x=-\sqrt{2}sinx\)
\(\Leftrightarrow\sqrt{2}sin\left(2x-\frac{\pi}{4}\right)=\sqrt{2}sin\left(-x\right)\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{4}\right)=sin\left(-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{4}=-x+k2\pi\\2x-\frac{\pi}{4}=\pi+x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
4.
Bạn coi lại đề, xuất hiện 2 số hạng \(cos4x\) ở vế trái nên chắc là bạn ghi nhầm
5.
\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=2cos^2\left(\frac{\pi}{4}-x\right)-1\)
\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=cos\left(\frac{\pi}{2}-2x\right)\)
\(\Leftrightarrow sinx.sin2x-cosx.sin^22x=sin2x\)
\(\Leftrightarrow sin2x\left(sinx-cosx.sin2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\Leftrightarrow x=...\\sinx-cosx.sin2x-1=0\left(1\right)\end{matrix}\right.\)
Xét (1):
\(\Leftrightarrow sinx-1-2sinx.cos^2x=0\)
\(\Leftrightarrow sinx-1-2sinx\left(1-sin^2x\right)=0\)
\(\Leftrightarrow2sin^3x-sinx-1=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(2sin^2x+2sinx+1\right)=0\)
\(\Leftrightarrow...\)

Chứng minh các biểu thức đã cho không phụ thuộc vào x.
Từ đó suy ra f'(x)=0
a) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
b) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
c) f(x)=\(\frac{1}{4}\)(\(\sqrt{2}\)-\(\sqrt{6}\))=>f'(x)=0
d,f(x)=\(\frac{3}{2}\)=>f'(x)=0

b)
(sin2x + cos2x)cosx + 2cos2x - sinx = 0
⇔ cos2x (cosx + 2) + sinx (2cos2 x – 1) = 0
⇔ cos2x (cosx + 2) + sinx.cos2x = 0
⇔ cos2x (cosx + sinx + 2) = 0
⇔ cos2x = 0
⇔ 2x = 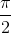 + kπ ⇔ x =
+ kπ ⇔ x = 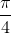 + k
+ k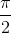 (k ∈
(k ∈ 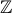 )
)
c)
Đáp án:
x=π6π6+ k2ππ
và x= 5π65π6+k2ππ (k∈Z)
Lời giải:
sin2x-cos2x+3sinx-cosx-1=0
⇔ 2sinxcosx-(1-2sin²x) +3sinx-cosx-1=0
⇔ 2sin²x+2sinxcosx+3sinx-cosx-2=0
⇔ (2sin²x+3sinx-2)+ cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+2)+cosx(2sinx-1)=0
⇔ (2sinx-1)(sinx+cosx+2)=0
⇔ sinx=1212
⇔ x=π6π6+ k2ππ
hoặc x= 5π65π6+k2ππ (k∈Z)
(sinx+cosx+2)=0 (vô nghiệm do sinx+cosx+2=√22sin(x+π4π4)+2>0)

6.
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)+\frac{1}{2}sinx.cosx=0\)
\(\Leftrightarrow1-3sin^2x.cos^2x+\frac{1}{2}sinx.cosx=0\)
\(\Leftrightarrow1-\frac{3}{4}sin^22x+\frac{1}{4}sin2x=0\)
\(\Leftrightarrow-3sin^22x+sin2x+4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=-1\\sin2x=\frac{4}{3}>1\left(l\right)\end{matrix}\right.\)
\(\Rightarrow2x=-\frac{\pi}{2}+k2\pi\)
\(\Rightarrow x=-\frac{\pi}{4}+k\pi\)
5.
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=\frac{5}{6}\left[\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\right]\)
\(\Leftrightarrow1-3sin^2x.cos^2x=\frac{5}{6}\left(1-2sin^2x.cos^2x\right)\)
\(\Leftrightarrow1-\frac{3}{4}sin^22x=\frac{5}{6}\left(1-\frac{1}{2}sin^22x\right)\)
\(\Leftrightarrow\frac{1}{3}sin^22x=\frac{1}{6}\)
\(\Leftrightarrow sin^22x=\frac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=\frac{\sqrt{2}}{2}\\sin2x=-\frac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{8}+k\pi\\x=\frac{3\pi}{8}+k\pi\\x=-\frac{\pi}{8}+k\pi\\x=\frac{5\pi}{8}+k\pi\end{matrix}\right.\)

c.
\(\Leftrightarrow sin\left(3x+\frac{2\pi}{3}\right)=-sin\left(x-\frac{2\pi}{5}-\pi\right)\)
\(\Leftrightarrow sin\left(3x+\frac{2\pi}{3}\right)=sin\left(x-\frac{2\pi}{5}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+\frac{2\pi}{3}=x-\frac{2\pi}{5}+k2\pi\\3x+\frac{2\pi}{3}=\frac{7\pi}{5}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{8\pi}{15}+k\pi\\x=\frac{11\pi}{60}+\frac{k\pi}{2}\end{matrix}\right.\)
d.
\(\Leftrightarrow cos\left(4x+\frac{\pi}{3}\right)=sin\left(\frac{\pi}{4}-x\right)\)
\(\Leftrightarrow cos\left(4x+\frac{\pi}{3}\right)=cos\left(\frac{\pi}{4}+x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+\frac{\pi}{3}=\frac{\pi}{4}+x+k2\pi\\4x+\frac{\pi}{3}=-\frac{\pi}{4}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{36}+\frac{k2\pi}{3}\\x=-\frac{7\pi}{60}+\frac{k2\pi}{5}\end{matrix}\right.\)
a.
\(sin\left(2x+1\right)=-cos\left(3x-1\right)\)
\(\Leftrightarrow sin\left(2x+1\right)=sin\left(3x-1-\frac{\pi}{2}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1-\frac{\pi}{2}=2x+1+k2\pi\\3x-1-\frac{\pi}{2}=\pi-2x-1+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+2+k2\pi\\x=\frac{3\pi}{10}+\frac{k2\pi}{5}\end{matrix}\right.\)
b.
\(sin\left(2x-\frac{\pi}{6}\right)=sin\left(\frac{\pi}{4}-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{6}=\frac{\pi}{4}-x+k2\pi\\2x-\frac{\pi}{6}=\frac{3\pi}{4}+x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{5\pi}{36}+\frac{k2\pi}{3}\\x=\frac{11\pi}{12}+k2\pi\end{matrix}\right.\)

Ta có:\(sin^6\left(\dfrac{x}{2}\right)-cos^6\left(\dfrac{x}{2}\right)\)=[sin2\(\left(\dfrac{x}{2}\right)\)-cos2\(\left(\dfrac{x}{2}\right)\)][sin4\(\left(\dfrac{x}{2}\right)\)+cos4\(\left(\dfrac{x}{2}\right)\)+sin2\(\left(\dfrac{x}{2}\right)\)+cos2\(\left(\dfrac{x}{2}\right)\)]=-cos(2.\(\dfrac{x}{2}\)){[sin2\(\left(\dfrac{x}{2}\right)\)+cos2\(\left(\dfrac{x}{2}\right)\)]2-sin2\(\left(\dfrac{x}{2}\right)\)cos2\(\left(\dfrac{x}{2}\right)\)}=-cosx[1-sin2\(\left(\dfrac{x}{2}\right)\)cos2\(\left(\dfrac{x}{2}\right)\)]
=-cosx[1-\(\dfrac{1}{4}\left(sin\left(\dfrac{x}{2}+\dfrac{x}{2}\right)+sin\left(\dfrac{x}{2}-\dfrac{x}{2}\right)\right)^2\)]
=-cosx(1-\(\dfrac{1}{4}sin^2x\))
=\(\dfrac{1}{4}cosx\left(sin^2x-4\right)\)
Câu này là chứng minh đẳng thức nhá!