Bỏ 20g tuyết(đá) có lẫn nước ở 0o vào nhiệt lượng kế chứa 250g nước ở 15o. Nhiệt độ nhiệt lượng kế giảm 5o. Nước lẫn trong tuyết là bao nhiêu? Biết nhiệt độ nch của nước đá là 3,3.10mũ5 j/kg, c nước là 4200j/kgk. Bỏ qua sự hấp thụ nhiệt của nhiệt lượng kế
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
14 tháng 8 2016
Hỗn hợp vừa có tuyết vừa có nước => ở 0 độ C
~O)~O) Q1 = Q2
0.25*4200*5 = (0.02 - m)*3,3*10^5 + 0.02*10*4200
=> 5250 = 840 + 6600 - 330000*m
=> m = 6.636 (g)
14 tháng 8 2016
Hỗn hợp vừa có tuyết vừa có nước => ở 0 độ C
~O)~O) Q1 = Q2
0.25*4200*5 = (0.02 - m)*3,3*10^5 + 0.02*10*4^200
=> 5250 = 840 + 6600 - 330000*m
=> m = 6.636 (g)
VT
17 tháng 4 2018
Gọi λ là nhiệt nóng chảy riêng của cục nước đá khối lượng m 0 , còn c 1 , m 1 , c 2 , m 2 là nhiệt dung riêng và khối lượng của cốc đồng và của lượng nước đựng trong cốc.
- Lượng nhiệt do cốc đồng và lượng nước đựng trong cốc ở t 1 = 25 ° C toả ra để nhiệt độ giảm tới t = 15,2 ° C có giá trị bằng :
Q = ( c 1 m 1 + c 2 m 2 ) ( t 1 -t)
- Lượng nhiệt do cục nước đá ở t 0 = 0 ° C thu vào để tan thành nước ở t = 15,2 ° C có giá trị bằng :
Q' = m 0 ( λ + c 2 t)
Theo nguyên lí cân bằng nhiệt, ta có :
Q' = Q ⇒ m 0 ( λ + c 2 t) = ( c 1 m 1 + c 2 m 2 ) ( t 1 -t)
Từ đó suy ra :
Thay số với chú ý m0 = 0,775 - 0,700 = 0,075 kg, ta tìm được :
VT
9 tháng 10 2019
Gọi λ là nhiệt nóng chảy riêng của cục nước đá khối lượng m 0 ở t 0 = 0 ° C ; còn c 1 , m 1 , c 2 , m 2 là nhiệt dung riêng và khối lượng của cốc nhôm và của lượng nước đựng trong cốc ở nhiệt độ t 1 = 20 ° C. Nếu gọi t ° C là nhiệt độ của nước trong cốc nhôm khi cục nước đá vừa tan hết thì lượng nhiệt do cục nước đá ở t 0 = 0 ° C đã thu vào để tan thành nước ở t ° C bằng :
Q = λ m 0 + c 2 m 0 (t - t 0 ) = m 0 ( λ + c 2 t)
Còn nhiệt lượng do cốc nhôm và lượng nước đựng trong cốc ở t 1 = 20 ° C. toả ra để nhiệt độ của chúng giảm tới toC (với t < t 1 ) có giá trị bằng :
Q'= ( c 1 m 1 + c 2 m 2 )( t 1 - t)
Theo định luật bảo toàn năng lượng, ta có :
Q' = Q ⇒ ( c 1 m 1 + c 2 m 2 ) ( t 1 - t) = m 0 ( λ + c 2 t)
Từ đó suy ra :
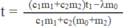
Thay số : t ≈ 3,7 ° C.
Q
28 tháng 7 2021
gọi m là số lượng kg nước cần thêm
nhiệt lượng để hệ tăng đến 0 độ
\(Q_1=0,1.2100.20+0,125.380.20=5150\left(J\right)\)
nhiệt lượng làm nửa đá tan
\(Q_2=3,4.10^5.\dfrac{0,1}{2}=17000\left(J\right)\)
cân bằng nhiệt ta có \(Q_1+Q_2=m.4200.20\Rightarrow m\approx0,264\left(kg\right)\)
22 tháng 12 2016
Khi được làm lạnh tới 00C, nước toả ra một nhiệt lượng bằng: Q1 = m1.C1(t – 0) = 0,5.4200.20 = 42 000JĐể làm “nóng” nước đá tới 00C cần tốn một nhiệt lượng:Q2 = m2.C2(0 – t2) = 0,5.2100.15 = 15 750JBây giờ muốn làm cho toàn bộ nước đá ở 00C tan thành nước cũng ở 00C cần một nhiệt lượng là: Q3 = λ.m2 = 3,4.105.0,5 = 170 000JNhận xét:+ Q1 > Q2 : Nước đá có thể nóng tới 00C bằng cách nhận nhiệt lượng do nước toả ra+ Q1 – Q2 < Q3 : Nước đá không thể tan hoàn toàn mà chỉ tan một phần.Vậy sau khi cân bằng nhiệt được thiết lập nước đá không tan hoàn toàn và nhiệt độ của hỗn hợp là 00C
16 tháng 10 2016
ta có:
nhiệt lượng nước đá cần để tan hết là:
\(Q_1=m_1\lambda=340000J\)
nhiệt lượng nước ở 5 độ C tỏa ra nếu nước đá chưa tan hết là:
\(Q_2=m_2C_2\left(t-t_2\right)=42000J\)
ta thấy Q2<Q1 nên nước đá chưa tan hết
\(\Rightarrow\) nhiệt độ hỗn hợp vẫn là 0 độ C
Hỗn hợp vừa có tuyết vừa có nước => ở 0 độ C
~O)~O) Q1 = Q2
0.25*4200*5 = (0.02 - m)*3,3*10^5 + 0.02*10*4200
=> 5250 = 840 + 6600 - 330000*m
=> m = 6.636 (g)
ban noi ro ra dc ko