Cho tứ diện ABCD có ABC và BCD là hai tam giác đều lần lượt nằm trong hai mặt phẳng vuông góc với nhau biết AD = a .Tính thể tích tứ diện
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 12 2018
Đáp án C
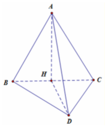
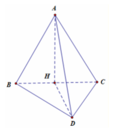
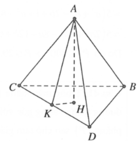
Gọi H là trung điểm của BC. Ta có: A H ⊥ B C
Mặt khác A B C ⊥ B C D ⇒ A H ⊥ B C D
Lại có A H = a 3 2 ⇒ V = 1 3 A H . S B C D = 1 3 . a 3 2 . a 2 3 4 = a 3 8
CM
25 tháng 2 2017
Đáp án D
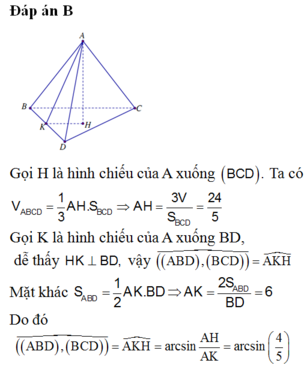
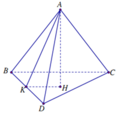
Gọi H là hình chiếu của A trên (BCD) ⇒ A H ⊥ B C D
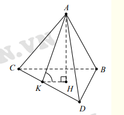Kẻ
H
K
⊥
C
D
K
∈
C
D
⇒
C
D
⊥
A
H
K
⇒
A
C
D
;
B
C
D
^
=
A
K
H
^
Ta có V A B C D = 1 3 A H . S ∆ B C D ⇒ A H = 3 V S ∆ B C D = 3 . 20 10 = 6
Và S ∆ A C D = 1 2 A K . C D ⇒ A K = 2 . S C D = 2 . 15 3 = 10
Tam giác AHK vuông tại H, có c o t A K H ^ = H K A H = 10 2 - 6 2 6 = 4 3
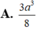
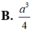
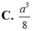
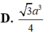
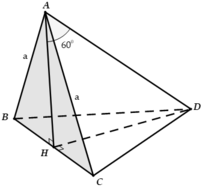
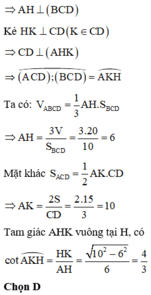
ban cm AH _|_mp (BCD) tương tự như trên ==> AH_|_DH, hai tg ABC va BCD la 2 tg đều có cạnh Bc chung nên đường cao của chúng bằng nhau=> tg HAD vuông cân tại H ma AD =a => Ah =Dh =sin45*a = a\(\frac{\sqrt{2}}{2}\)
tg đều biết độ dài đường cao => độ dài mỗi cạnh, tu do tinh duoc dt tg ABC va tinh duoc the tich khoi chopbạn tự vẽ hình và tính nah