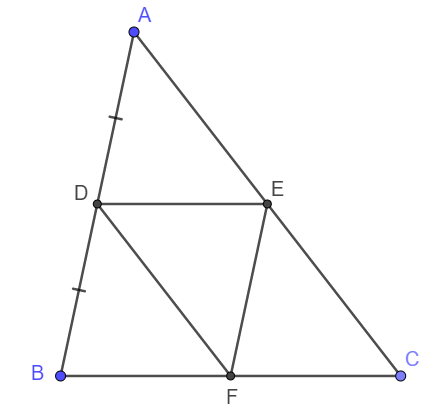
Cho tam giác ABC, D là trung điểm của cạnh AB. Đường thẳng qua B song sog vs cạnh BC cắt AC ở E, đường thẳng qua E sog sog với cạnh AB cắt BC ở F. cmr:
a)AD=EF
b)AE=EC, BF=FC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
2 tháng 3 2018
a) Xét tam giác DEF và tam giác FBD có:
Cạnh DF chung
\(\widehat{EDF}=\widehat{BFD}\) (Hai góc so le trong)
\(\widehat{EFD}=\widehat{BDF}\) (Hai góc so le trong)
\(\Rightarrow\Delta DEF=\Delta FBD\left(g-c-g\right)\Rightarrow EF=BD=AD\)
b)
Xét tam giác ADE và tam giác EFC có:
\(\widehat{DAE}=\widehat{FEC}\) (Hai góc so le trong)
\(\widehat{EFC}=\widehat{ADE}\left(=\widehat{DBF}\right)\)
\(\Rightarrow\Delta ADE=\Delta EFC\left(g-c-g\right)\Rightarrow AE=EC\)
Từ đó ta cũng suy ra DE = FC
Lại có do \(\Delta DEF=\Delta FBD\Rightarrow DE=FB\)
Vậy nên FC = FB
c) Ta có FC = FB = DE nên \(DE=\frac{BC}{2}\)
EF = AD = DB nên \(EF=\frac{AB}{2}\)
11 tháng 2 2018
Bn ơi, cho mk hỏi tí! Cái chỗ góc A = góc DBM ( 2 góc tương ứng ) sao có thể suy ra AC // MB, bn có thể lm rõ hơn chỗ đó cho mk đc ko
29 tháng 7 2016
a) Xét tam giác CEF và tam giác FBD có:
- DF là cạnh chung
- Góc EDF = góc DFB ( Hai góc so le nhau trong của DE//BC )
- Góc BDF = góc EDF ( Hai góc so le nhau trong của EF//AB )
=> Tam giác CEF = tam giác FBD ( g.c.g )
=> EF = DB ( 2 cạnh tương ứng )
Mà BD = AD ( D là trung điểm của AB )
=> EF = AD
Vậy AD = EF
b)
Vì tam giác ADE = tam giác EFC
=> AE = EC ( vì 2 cạnh tương ứng )
TN
29 tháng 7 2016
BẠN TỰ VẼ HÌNH NHA!!
a. Xét \(\Delta CEF\) và \(\Delta FBD\) có :
DF chung
\(\widehat{EDF}=\widehat{DEB}\) ( 2 góc so le trong )
\(\widehat{BDF}=\widehat{EDF}\) ( 2 góc so le trong)
\(\Rightarrow\Delta CEF=\Delta FBD\) ( g.c.g)
\(\Rightarrow\) EF=DB (2 cạch tương ứng)
mà BD=AD (D là trung điểm của AB
\(\Rightarrow\) AD=EF
29 tháng 1 2023
a: Xét ΔABC có
D là trung điểm của AB
DE//BC
=>E là trung điểm của AC
=>AE=EC
Xét ΔCAB có
E là trung điểm của CA
EF//AB
=>F là trung điểm của BC
=>FB=FC
b: Xét ΔABC có D,E lần lượt là trung điểm của AB,AC
nên DE là đường trung bình
=>ED=1/2BC
Xét ΔCAB có CF/CB=CE/CA
nên EF//AB
=>FE/AB=CF/CB=1/2
=>FE=1/2AB
a: Xét tứ giác ADFE có
AD//FE
AE//DF
Do đó: ADFE là hình bình hành
Suy ra: AD=EF
b: Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
hay AE=EC
Xét ΔABC có
E là trung điểm của AC
EF//AB
Do đó: F là trung điểm của BC
hay BF=FC