1, Trong mặt phẳng Oxy cho tam giác ABC có A(1;6) trực tâm H(1;2) tâm đường tròn ngoại tiếp tam giác là I(2;3) .Tìm tọa độ B,C biết B có hoành độ dương
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B → = 3 ; 12 , A C → = 4 ; − 1 ⇒ ( A B ) ⃗ . ( A C ) ⃗ = 3 . 4 + 12 . ( - 1 ) = 0 ⇒ ∆ A B C vuông tại A. Trực tâm của tam giác là đỉnh A. Chọn B

\(\left\{{}\begin{matrix}\overrightarrow{BA}=\left(3;-1\right)\\\overrightarrow{BC}=\left(-4;-2\right)\end{matrix}\right.\)
\(\Rightarrow cos\widehat{ABC}=cos\left(\overrightarrow{BA};\overrightarrow{BC}\right)=\dfrac{3.\left(-4\right)+1.2}{\sqrt{3^2+1^2}.\sqrt{\left(-4\right)^2+\left(-2\right)^2}}=-\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{ABC}=135^0\)

\(AB=\sqrt{\left(5-1\right)^2+\left(-3+1\right)^2}=2\sqrt{5}\)
\(AC=\sqrt{\left(0-1\right)^2+\left(1+1\right)^2}=\sqrt{5}\)
\(BC=\sqrt{\left(0-5\right)^2+\left(1+3\right)^2}=\sqrt{29}\)
=>C=3 căn 5+căn 29

Ta có B A → = 3 ; − 1 và B C → = − 4 ; − 2 . Suy ra:
cos B A → , B C → = B A → . B C → B A → . B C → = 3. − 4 + − 1 . − 2 9 + 1 . 16 + 4 = − 2 2 ⇒ B ^ = B A → , B C → = 135 O .
Chọn D.

\(AB=\sqrt{\left(0+1\right)^2+\left(2+3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left(2+1\right)^2+\left(1+3\right)^2}=\sqrt{3^2+4^2}=5\)
\(BC=\sqrt{\left(2-0\right)^2+\left(1-2\right)^2}=\sqrt{5}\)
=>\(C=\sqrt{26}+5+\sqrt{5}\left(cm\right)\)

\(\overrightarrow{AB}=\left(1;-2\right)\Rightarrow AB=\sqrt{5}\)
\(\overrightarrow{AC}=\left(-2;2\right)\Rightarrow AC=2\sqrt{2}\)
\(BC=\left(-3;4\right)\Rightarrow BC=5\)
Chu vi tam giác ABC: \(AB+AC+BC=\sqrt{5}+2\sqrt{2}+5\)

Ta có A B → = 2 ; − 2 B C → = 2 ; 2 C A → = − 4 ; 0 ⇒ A B = 2 2 + − 2 2 = 2 2 B C = 2 2 + 2 2 = 2 2 C A = − 4 2 + 0 2 = 4
Vậy chu vi P của tam giác ABC là P =AB + BC + CA = 4 + 4 2
Chọn B.

Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2) 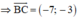
Phương trình đường cao AH đi qua A(2;-1) nhận 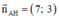 là VTPT là:
là VTPT là:
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.

vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1
Lời giải:
Gọi \(B(a,b)\) và \(C(c,d)\)
Ta có \(\overrightarrow {HA}=(0,4)\perp \overrightarrow{BC}=(c-a,d-b)\Rightarrow 4(d-b)=0\rightarrow b=d\)
Thay \(d=b\):
\(\overrightarrow{HB}=(a-1,b-2)\perp \overrightarrow{AC}=(c-1,b-6)\)
\(\Rightarrow (a-1)(c-1)+(b-2)(b-6)=0\)
Lại có \(IA^2=IB^2=IC^2\leftrightarrow\left\{{}\begin{matrix}\left(a-2\right)^2+\left(b-3\right)^2=10\\\left(c-2\right)^2+\left(b-3\right)^2=10\end{matrix}\right.\)
\(\Rightarrow (a-2)^2=(c-2)^2\rightarrow a+c=4\) ( \(a\neq c\) )
Ta thu được
\(\left\{{}\begin{matrix}\left(a-2\right)^2+\left(b-3\right)^2=10\\\left(3-a\right)\left(a-1\right)+\left(b-2\right)\left(b-6\right)=0\end{matrix}\right.\)
\(\left\{\begin{matrix} a^2+b^2-4a-6b+3=0\\ -a^2+4a+b^2-8b+9=0\end{matrix}\right.\Rightarrow 2b^2-14b+12=0\rightarrow b=1\)
hoặc \(b=6\)
Thay vào PT suy ra \(\left[{}\begin{matrix}-a^2+4a+2=0\\-a^2+4a-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}a=2+\sqrt{6}\\a=1;a=3\end{matrix}\right.\)
Vậy.....
cj em nói cj này giỏi thiệt còn em k bit j