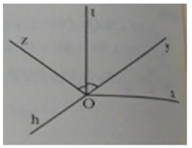
Cho góc bẹt xOy. Trên cùng một nửa mặt phẳng bờ xy vẽ hai tia Ot ,Oz và trên nửa mặt phẳng kia vẽ tia Oh sao cho xOz = yOt = xOh = 50 độ. Các cặp góc sau xOz và xOh; xOz và yOt; xOh và yOt có đối đỉnh không? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\widehat{xOz}\)và \(\widehat{xOh}\)ko phải là 2 góc đối đỉnh. Vì 2 góc đó ở vị trí kề nhau
b) \(\widehat{xOz}\)và \(\widehat{yOt}\) ko phải là 2 góc đối đỉnh. Vì nó ko là tia đối của một cạnh của góc kia
c) \(\widehat{xOh}\)và \(\widehat{yOt}\)là 2 góc đối đỉnh vì hai góc đối đỉnh mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia
mình cần một lời giải chi tiết hơn
chứ thế này thì mình cũng biết

`Answer:`
a, Theo đề ra: Tia `Ox` và tia `Oy` là hai tia đối nhau nên `\hat{xOt}+\hat{yOt}=180^o` (Kề bù)
`=>\hat{xOt}+ 55^o =180^o`
`=>\hat{xOt}=125^o`
Ta có: `\hat{xOz}=70^o;\hat{xOt}=125^o=>\hat{xOz}<\hat{xOt}=>` Tia `Oz` nằm giữa hai tia `Ox` và `Ot`
b, Theo đề ra: Tia `Ox` và tia `Oy` là hai tia đối nhau nên `\hat{xOz}+ \hat{zOy}=180^o` (Kề bù)
`=>70^o+ \hat{zOy}=180^o`
`=>\hat{zOy}=110^o`
Ta có: `\hat{yOt}=55^o;\hat{yOz}=110^o=>\hat{yOt}<\hat{yOz}=>` Tia `Ot` nằm giữa hai tia `Oy` và `Oz` (*)
Ta có: `\hat{yOt}+ \hat{zOt}=\hat{yOz}`
`=>55^o +\hat{zOt}=110^o`
`=>\hat{zOt}=55^o`
Mà `\hat{yOt}=55^o=>\hat{yOt}=\hat{zOt}=55^o` (**)
Từ (*)(**)`=>Ot` là tia phân giác của `\hat{yOz}`
c, Theo đề ra: `On` là tia phân giác của `\hat{xOz}`
`=>\hat{nOz}=\hat{xOz}:2=70^o :2=35^o`
Ta có: `\hat{nOt}=\hat{nOz}+\hat{zOt}=35^o +55^o =90^o`

a)Hai tia Oy, Oz cùng thuộc nửa mặt phẳng chứa tia Ox và
x O y ^ = 50 < x O z ^ = 130
⇒ Tia Oy nằ, giữa hai tia Ox, Oz nên: x O y ^ + y O z ^ = x O z ^
⇒ y O z ^ = 130 - 50 = 80
b)Do đó Ot là tia phân giác y O z ^ n ê n : y O t ^ = y O z ^ = 40
Tia Oy nằm giữa hai tia Ox, Ot nên:
x O t ^ = x O y ^ + y O t ^ = 50 + 40 = 90
c)Ta có: x O y ^ + x O h ^ = 180
( x O y ^ v à x O h ^ là hai góc kề bù)
⇒ x O h ^ = 180 - x O y ^ = 130
Vậy x O y ^ = x O h ^ ( = 130 )

zOt+xOz+yOt=180 độ (xOy=180 độ)
zOt+35+55=180
zOt=180-90
zOt=90
Vì zOt=90 độ nên Oz vuông góc Ot tại O

b) Ta có: tia Oz nằm giữa hai tia Ox và Ot(cmt)
nên \(\widehat{xOz}+\widehat{tOz}=\widehat{xOt}\)
\(\Leftrightarrow\widehat{tOz}+70^0=125^0\)
hay \(\widehat{tOz}=55^0\)
Ta có: \(\widehat{xOz}+\widehat{yOz}=180^0\)(hai góc kề bù)
\(\Leftrightarrow70^0+\widehat{yOz}=180^0\)
hay \(\widehat{yOz}=110^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia Oy, ta có: \(\widehat{yOt}< \widehat{yOz}\left(55^0< 110^0\right)\)
nên tia Ot nằm giữa hai tia Oy và Oz
Ta có: tia Ot nằm giữa hai tia Oy và Oz(cmt)
mà \(\widehat{yOt}=\widehat{zOt}\left(=55^0\right)\)
nên Ot là tia phân giác của \(\widehat{yOz}\)(đpcm)
a) Ta có: \(\widehat{yOt}+\widehat{xOt}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{xOt}+55^0=180^0\)
hay \(\widehat{xOt}=125^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOz}< \widehat{xOt}\left(70^0< 125^0\right)\)
nên tia Oz nằm giữa hai tia Ox và Ot(Đpcm)