Cho mạch điện gồm cuộn dây có điện trở r=70Ω và L=0.7H nối tiếp với tụ điện có điện dung C thay đổi được. Đặt vào hai đầu mạch điện một điện áp U=140cos(100t-π/2)V. Khi C=Co thì U cùng pha với cường độ dòng điện I trong mạch. Khi đó biểu thức điện áp giữa hai đầu cuộn dây Ud là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
+ Khi

mạch tiêu thụ công suất cực đại → Z C 1 = Z L = 160 Ω
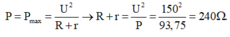
+ Khi
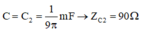
thì điện áp hai đầu cuộn dây vuông pha với điện áp hai đầu RC.

=> R = r = 120 Ω
+ Điện áp hiệu dụng hai đầu cuộn dây khi đó là:
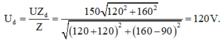

Đáp án B
Phương pháp: Sử dụng định luật Ôm, chú ý điều kiện cộng hưởng.
Cách giải
Khi C = C1, u cùng pha với I, trong mạch có cộng hưởng.
UAB = UR; ULR = 60V
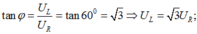
![]()

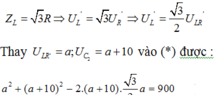
![]()
Chọn đáp án gần giá trị a = 49,86V = 50V

Đáp án B
Phương pháp: Sử dụng định luật Ôm, chú ý điều kiện cộng hưởng.
Cách giải:
Khi C = C 1 , u cùng pha với I, trong mạch có cộng hưởng.
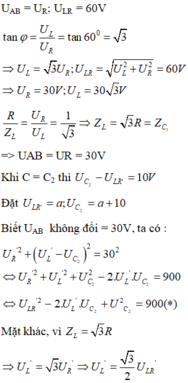
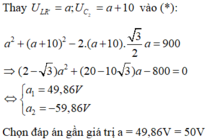

Đáp án B
Phương pháp: Sử dụng định luật Ôm, chú ý điều kiện cộng hưởng.
Cách giải: Khi C = C1, u cùng pha với I, trong mạch có cộng hưởng. UAB = UR; ULR = 60V

![]()
![]()
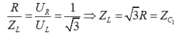
![]()
Khi
C
=
C
2
thì ![]()
Đặt
![]()
. Biết U AB không đổi = 30V, ta có:
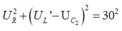
![]()
![]()
Mặt khác,vì
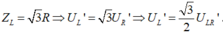
Thay ![]() vào biểu thức (*) ta được:
vào biểu thức (*) ta được:
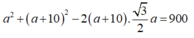
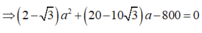
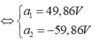
Chọn đáp án gần giá trị a = 49,86V = 50V. Đáp án B

Chọn đáp án A
Khi độ tự cảm L1 = 1/π H thì i cùng pha với u => Mạch xảy ra cộng hưởng => ZL1 = ZC.
Khi L2 = 2/π H thì UL đạt cực đại

![]()
![]()
![]()
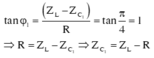
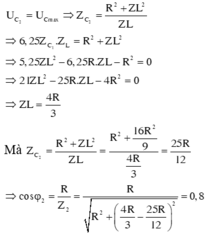


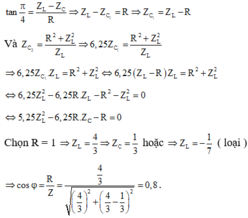
U cùng pha với I tức là xảy ra hiện tượng cộng hường \(Z_L=Z_C\)
=> \(Z=r=70\Rightarrow I_0=\frac{U_0}{Z}=\frac{140}{70}=2A.\)
\(Z_L=L\omega=70\Omega.\)
\(U_{0\left(L,r\right)}=I\sqrt{r^2+Z_L^2}=2.70\sqrt{2}=140\sqrt{2}V.\)
\(\tan\varphi=\frac{Z_L}{r}=\frac{70}{70}=1\Rightarrow\varphi=\frac{\pi}{4}.\)
=> \(\varphi_{u\left(L,r\right)}-\varphi_i=\varphi_{u\left(L,r\right)}-\varphi_u=\frac{\pi}{4}\Rightarrow\varphi_{u\left(L,r\right)}=\frac{\pi}{4}-\frac{\pi}{2}=-\frac{\pi}{4}.\)
=> phương trình u dây là \(u_{L,r}=140\sqrt{2}\cos\left(100t-\frac{\pi}{4}\right)V.\)