Hai dao động điều hòa có phương trình x1 = A1cos ω1t và x2 = A2 cos ω2t được biểu diễn trong một hệ tọa độ vuông góc xOy tương ứng bằng hai vectơ quay A1 mà hai vectơ A1 và A2. Trong cùng một khoảng thời gian, góc và A2 quay quanh O lần lượt là α1 và α2 = 2,5α1. Tỉ số ω1 / ω2 là:
A. 2,0
B. 2,5
C. 1,0
D. 0,4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


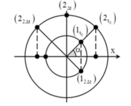
Với giả thuyết sau khoảng thời gian 2 ∆ t dao động 1 quay trở về vị trí ban đầu → có hai trường hợp hoặc 2 ∆ t = T khi đó 1 đi đúng 1 vòng, hoặc 2 ∆ t ≠ T .
+ Ta biểu diễn hai trường hợp tương ứng trên đường tròn. Với 2 ∆ t = T dễ dàng thấy rằng ω 1 = ω 2 .
+ Với trường hợp 2 ∆ t ≠ T sau khoảng thời gian ∆ t vật 1 đến biên, vật 2 đó đi qua vị trí cân bằng, khoảng cách giữa hai vật lúc này là 2 a → A 1 = 2 a
Theo giả thuyết bài toán:
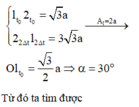
Đáp án A

Đáp án B
Vị trí của 2 vật tại các thời điểm:
+ Tại thời điểm ban đầu: A 2 cos φ - A 1 cos φ = a 3 ( 1 )
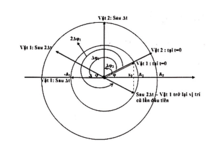
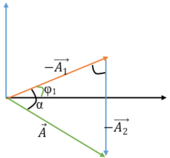
+ Sau ∆ t : (2 dao động biểu diễn bằng 2 vectơ quay): Vật 1 quay góc ∆ φ 1 , vật 2 quay góc ∆ φ 2 (vì vật 1, sau 2 ∆ t là góc 2 ∆ φ 1 thì nó trở lại vị trí cũ x 0 lần đầu nên sau (góc quay ) nó phải ở -A1 như hình vẽ. Vật 2 chuyển động chậm hơn, và vuông pha với vật 1 nên ở vị trí như hình vẽ). Khoảng cách 2 vật lúc này là: A1 = 2a (2)
+ Sau 2 ∆ t , vật 1 quay thêm góc ∆ φ 2 nữa, vật 2 quay góc nữa. Chúng biểu diễn bằng các vectơ. Khoảng cách của chúng:
A 2 cos φ + A 1 cos φ = 3 a 3
+ Theo hình vẽ:
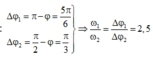

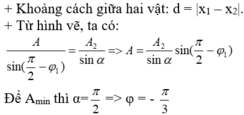
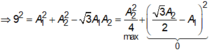
Đáp Án Câu E nha Bạn. Mình Làm Bài Này 69 Lần Rồi
Đâu ra câu E?