Trong thí nghiệm giao thoa chiếu đồng hai hai bức xạ có bước sóng lần lượt là 420nm và 525nm. Hệ vân giao thoa trên màn , tại điểm M là vân sáng bậc 4 của bức xạ lamda1 và điểm N vân sáng bậc 11 của bức xạ lamda2. Điểm MN nằm cùng phái so với vân trung tâm. Tìm số vân sáng trong khoảng MN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 1 2016
Ta có:
\(\dfrac{i_1}{i_2}=\dfrac{\lambda_1}{\lambda_2}=\dfrac{2}{3}\)
Theo giả thiết:
\(x_M=6i_1=6.\dfrac{2}{3}i_2=4i_2\)
\(x_N=6i_2=6.\dfrac{3}{2}i_1=9i_1\)
Như vậy, trung điểm I có tọa độ: \(x_I=7,5i_1=5i_2\)
Do đó, trong khoảng giữa I và N có vân i1 là: \(8i_1\), và không có vân i2 nào
Như vậy, tổng cộng có 1 vân sáng.
HD
Hà Đức Thọ
Admin
20 tháng 11 2015
\(\frac{i_1}{i_2}=\frac{\lambda_1}{\lambda_2}=\frac{0,6}{0,45}=\frac{4}{3}\)
\(x_M=3i_1=3.\frac{4}{3}i_2=4i_2\)
\(x_N=8i_2=8.\frac{3}{4}i_1==6i_1\)
+ Không tính M, N thì trên đoạn MN có các vạch sáng là: \(4i_1,5i_1;5i_2,6i_2,7i_2\)
+ Tìm số vị trí vân trùng nhau của \(\lambda_1,\lambda_2\):
\(x_T=k_1i_1=k_2i_2\Rightarrow\frac{i_1}{i_2}=\frac{k_2}{k_1}=\frac{4}{3}\)
\(\Rightarrow k_2=4\)
Như vậy, các vị trí trùng nhau là: \(4i_2,8i_2,12i_2,...\)
Do đó, hai đầu mút là các vị trí trùng nhau (\(4i_2\), và \(8i_2\)) nhưng không tính
Vậy tổng số các vị trí trùng nhau là: 5
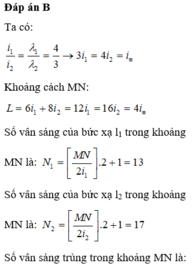
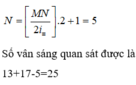
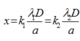
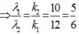
Ta có:
\(\dfrac{i_1}{i_2}=\dfrac{\lambda_1}{\lambda_2}=\dfrac{4}{5}\)
\(x_M=4i_1=4.\dfrac{4}{5}i_2=3,2.i_2\)
\(x_N=11i_2=11.\dfrac{5}{4}i_1=13,75i_1\)
Vậy từ M đến N có:
+ Số vân i1 là: 5i1, 6i1, ..., 13i1 --> 9 vân
+ Số vân i2 là: 4i2, 5i2, ..., 10i2 -->7 vân
+ Số vân trùng nhau: Không có (do vân trùng nhau cách nhau 20i1)
Vậy tổng số vân sáng là: 9 + 7 = 16 vân.