Câu 1: Dòng điện tức thời có biểu thức \(i=4cos^2\left(\omega t\right)\left(A\right)\) có giá trị hiệu dụng là ? (T ko biết cái biểu thức cos bình là như nào :3)
Câu 2: Mạch RLC nối tiếp có C thay đổi được. Điện áp 2 đầu đoạn mạch là u=\(150\sqrt{2}cos\left(100\pi t\right)\left(V\right)\). Khi C=C1=\(\frac{62.5}{\pi}\left(\mu F\right)\) thì mạch có công suất cực đại = 93.75W. Khi C=C2=\(\frac{1}{9\pi}\left(mF\right)\) thì điện áp 2 đầu đoạn mạch RC và cuộn dây vuông pha với nhau. Điện áp hiệu dụng giữa 2 đầu cuộn dây khi đó là ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
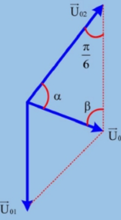
Đoạn mạch AB gồm AM nối tiếp MB nên ta có: ![]() (hình vẽ)
(hình vẽ)
Mà u 1 nhanh pha hơn u 2 một góc 5 π 6 rad nên ta có các góc như hình vẽ.
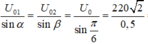
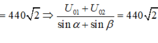

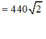
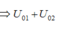
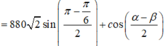
![]()
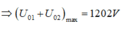

* Ban đầu: \(\varphi_{u/i}=-\dfrac{\pi}{4}-(-\dfrac{\pi}{2})=\dfrac{\pi}{4}(rad)\)
\(\Rightarrow \tan\varphi = \dfrac{-Z_C}{R}=-1\Rightarrow Z_C= R\)
Tổng trở của mạch: \(Z=\sqrt{R^2+Z_C^2}=R\sqrt 2\)
* Khi mắc nối tiếp vào mạch tụ thứ 2 có điện dung bằng điện dung đã cho thì: \(Z_C'=2Z_C=2R\)
Tổng trở: \(Z'=\sqrt{R^2+Z_C'^2}=\sqrt{R^2+(2R)^2}=R\sqrt 5\)
\(\Rightarrow \dfrac{I'}{I}=\dfrac{Z}{Z'}=\dfrac{\sqrt 2}{\sqrt 5}\)
\(\Rightarrow I'=0,63I\)
\(\Rightarrow I_0'=0,63I_0\)
Độ lệch pha giữa u và i: \(\tan\varphi = \dfrac{-Z_C'}{R}=2\)
\(\Rightarrow \varphi{_{u/i}} = -0,352\pi(rad)\Rightarrow \varphi{_{i/u}} = 0,352\pi(rad)\)
\(\Rightarrow \varphi i'=\varphi _u+0,352\pi=-0,5\pi+0,352\pi=-0,147\pi\)(rad)
Vậy biểu thức của dòng điện là:
\(i=0,63I_0\cos(\omega t -0,147\pi) (A)\)
Chọn A.

Ta có: \(Z_C=\frac{1}{C\omega}=30\Omega\)
\(\tan\varphi=-\frac{Z_c}{R}=-\frac{1}{\sqrt{3}}\)
\(\Rightarrow\varphi=-\frac{\pi}{6}\)
\(\Rightarrow\varphi_U-\varphi_I=-\frac{\pi}{6}\Rightarrow\varphi_1=\frac{\pi}{6}rad\)
Lại có: \(I=\frac{U}{Z}=2\sqrt{2}\left(A\right)\)
\(\Rightarrow i=2\sqrt{2}\cos\left(100\pi t+\frac{\pi}{6}\right)\left(A\right)\)
Đáp án A

Giải thích: Đáp án C
Lúc đầu chưa mắc C, mạch chỉ có RL: 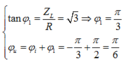
*Khi mắc thêm C:
![]() => Mạch xảy ra hiện tượng cộng hưởng.
=> Mạch xảy ra hiện tượng cộng hưởng.
![]()

\(\varphi=\varphi_u-\varphi_i=0-\left(-\frac{\pi}{4}\right)=\frac{\pi}{4}\)
\(\tan\varphi=\frac{Z_L-Z_C}{R}=1\Rightarrow Z_L-Z_C=R\)
\(\Rightarrow Z=\sqrt{R^2+\left(Z_L-Z_C\right)^2}=R\sqrt{2}\)
Mà \(Z=\frac{U}{I}=\frac{200}{2}=100\Rightarrow R=\frac{100}{\sqrt{2}}=50\sqrt{2}\)

Giải thích: Đáp án D
Phương pháp: Sử dụng lí thuyết về mạch điện có C thay đổi
Cách giải:
+ Khi C = C1 và C = C2 thì: 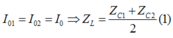
+ Khi C = C3 thì cường dộ dòng điện trong mạch có giá trị hiệu dụng đạt cực đại => ZL = ZC3 (2)
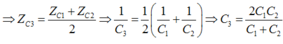
+ Khi C = C1 và C = C2 :
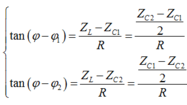
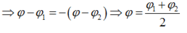
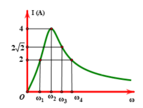
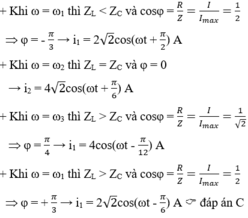
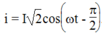 i = I
i = I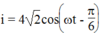
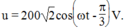
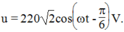



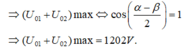
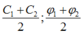
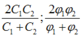
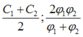
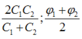
Câu 1 bạn dùng công suất trung bình để tìm I hiệu dụng nhé, mà cái này không thi đâu.