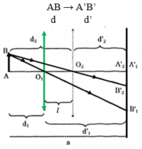
Vật sáng AB được đặt song song với màn và cách màn một khoảng cố định a. Một thấu kính hội tụ có trục chính qua điểm A và vuông góc với màn, được di chuyển giữa vật và màn.
a) Người ta thấy có một vị trí của thấu kính cho ảnh rõ nét của vật trên màn, ảnh lớn hơn vật. Hãy chứng tỏ rằng, có một vị trí thứ hai của thấu kính ở trong khoảng giữa vật và màn cũng cho ảnh rõ nét của vật trên màn.
b) Đặt l là khoảng cách giữa hai vị trí trên của thấu kính. Hãy lập công thức của tiêu cự thấu kính f theo a và l. Suy ra một phương pháp đo tiêu cự của thấu kính hội tụ.

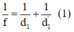
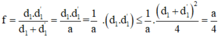

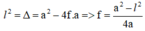
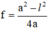

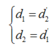
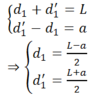
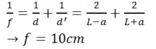
a) Chứng minh:
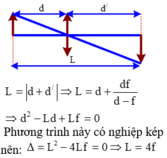
\(d+d' =a \Rightarrow d' = a -d\)
Và \(f=\frac{d.d'}{d+d'} \Rightarrow d = \frac{d.(a-d)}{a}\)
\( \Rightarrow d^2 -ad + af =0\)
\( \Delta = a^2 -4af =a(a-4f)\)
(Điều kiện để phương trình có nghiệm là \(a \geq 4f \))
Vì đã có 1 ảnh rõ nét rồi nên phương trình sẽ có nghiệm, vì có vị trí thứ 2 nữa nên phương trình phải có 2 nghiệm phân biệt.
Ta có hai vị trí này là 2 nghiệm có phương trình:
\( d_1 = \frac{a+ \sqrt{\Delta}}{2}\)
\(d_2 = \frac{a- \sqrt{\Delta}}{2}\)
b) Gọi l =khoảng cách 2 vị trí trên ta có:
\( l = d_2 -d_1 = \frac{a+ \sqrt { \Delta} - (a- \sqrt { \Delta})}{2} = \sqrt{\Delta} \)
Ta có: \(l^2 = \Delta = a^2 -4af \Rightarrow f = \frac{a^2 -l^2 }{4a}\)
Để đo tiêu cự chỉ cần đo khoảng cách giữa 2 vị trị cho ảnh rõ nét trên màn và khoảng cách giữa vật- màn. Phương pháp này gọi là phương pháp Bessel. Hoặc có thể dùng bất đẳng thức Cauchy để chứng minh cũng được nhé!