C2. Hãy giải thích tại sao khi cho nam châm (hoặc cuộn dây) quay thì ta lại thu được dòng điện xoay chiều trong các máy trên khi nối hai cực của máy với các dụng cụ tiêu thụ điện.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì số đường sức từ xuyên qua tiết diện S của cuộn dây dẫn luân phiên tăng giảm khi nam châm hoặc cuộn dây quay.

Đáp án D
Khi quay nam châm của máy phát thì trong cuộn dây của nó xuất hiện dòng điện xoay chiều vì số đường sức từ qua tiết diện S của cuộn dây luân phiên tăng giảm.

Nối hai cực của máy phát điện xoay chiều với một bóng đèn. Khi quay nam châm của máy phát thì trong cuộn dây của nó xuất hiện dòng điện cảm ứng xoay chiều vì số đường sức từ qua tiết diện S của cuộn dây luân phiên tăng giảm
→ Đáp án D

Đáp án C
Ta có : 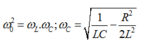
Ta có: 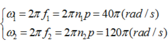
Điện áp hiệu dụng hai đầu cuộn cảm
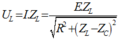
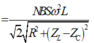
Khi
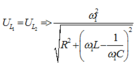
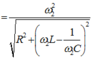
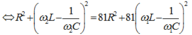
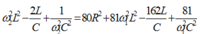
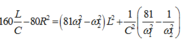
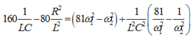
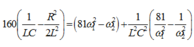
Lại có 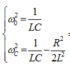
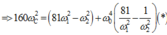
Thay ![]() vào (*) ta có :
vào (*) ta có :
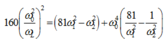
Thay số ta có
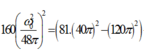
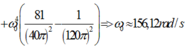

Đáp án C
Chú ý E tỉ lệ thuận với n. Chuẩn hóa R = 1. Áp dụng công thức tính ![]()

Công suất của mạch ngoài \(P = I^2 R = \frac{E^2}{R^2+(Z_L-Z_C)^2}R\)
Mà suất điện động hiệu dụng \(E = \omega\Phi \)
TH1: \(\omega = \omega_0; P_{max}\)
\(P = I^2 R = \frac{E^2}{R^2+(Z_L-Z_C)^2}R\)
\( = \frac{\omega^2 \Phi ^2}{R^2+(Z_L-Z_C)^2}R \)
\( = \frac{ \Phi ^2}{\frac{R^2}{\omega^2}+\frac{Z_L^2}{\omega^2}-2\frac{Z_LZ_C}{\omega^2}+\frac{Z_C^2}{\omega^2}}R \)
\( = \frac{ \Phi ^2}{\frac{1}{\omega^4C^2}+\frac{R^2-2L/C}{\omega^2}+L^2}R \)
\(P_{max} \Leftrightarrow A = (\frac{1}{\omega^4C^2}+\frac{R^2-2L/C}{\omega^2}+L^2)_{min}\)
đặt \(x = \frac{1}{\omega^2}\)
=> \(A_{min} \Leftrightarrow x = \frac{-b}{2a} = \frac{2L/C-R^2}{2/C^2}.\)
=> \(\frac{2}{C^2\omega_0^2} = \frac{2L}{C}-R^2\) hay \(2Z_C^2 = 2Z_LZ_C - R^2 => R^2 =2Z_LZ_C- 2Z_C^2.(1)\)
Ta có \(\frac{P_1}{P_0} = \frac{I_1^2}{I_0^2} = \frac{E_1^2Z_0^2}{E_0^2Z_1^2} = \frac{\omega_1^2Z_0^2}{\omega_0^2Z_1^2} = \frac{4\omega_0^2Z_0^2}{\omega_0^2Z_1^2} = \frac{1}{2}\)
=> \(Z_1^2 = 8Z_0^2\)
=> \(R^2 +(2Z_L - \frac{Z_C}{2})^2 = 8 (R^2 + (Z_L-Z_C)^2) (2)\)
Thay (1) vào (2) ta được \(4Z_L^2 -\frac{7Z_C^2}{4} = 8(Z_L^2 - Z_C^2)\)
=> \(\frac{25}{4}Z_C^2 = 4Z_L^2\) hay \(Z_L = \frac{5}{4}Z_C .(3)\)
Tiếp theo ta xét tỷ số \(\frac{P_2}{P_0} = \frac{\omega_2^2 Z_0^2}{\omega_0^2Z_2^2} = \frac{9.(R^2+(Z_L-Z_C)^2)}{R^2+(3Z_L-Z_C/3)^2}=\frac{9(Z_L^2 - Z_C^2)}{9Z_L^2 - 17/9Z_C^2} = \frac{9(25/4-1)}{9.25/4 - 17/9} = \frac{81/16}{1753/144} = \frac{729}{1753}.\)
=> \(P_2 = \frac{729}{1753}P_0\)
Đáp án thu được như của bạn rồi nhé.

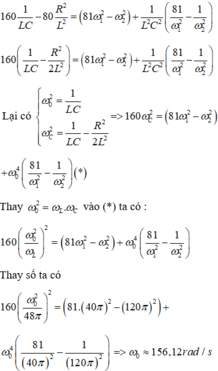



Khi cho nam châm (cuộn dây quay) thì số đường sức từ qua tiết diện S của cuộn dây luân phiên tăng giảm, do đó trong cuộn dây xuất hiện dòng điện xoay chiều.
Khi cho nam châm (cuộn dây quay) thì số đường sức từ qua tiết diện S của cuộn dây luân phiên tăng giảm, do đó trong cuộn dây xuất hiện dòng điện xoay chiều.