Con lắc đơn gồm 1 dây kim loại nhẹ có đầu trên cố định, đầu dưới treo một vật nhỏ. chiều dài của dây treo là 20cm
con lắc dao động điều hòa với anpha0=0,15 rad. Con lắc dao động trong từ trường đều, vecto cảm ứng từ B vuông
góc với mặt phẳng dao động của con lắc. B= 0,5T, g=9,8 m/s2. Suất điện động cực đại xuất hiện trên dây kim loại là:
A. 17 mV B. 21mV C. 8,5 mV D. 10,5 mV
-trong sách giải có trình bày như này ạ:
Suất điện động trên dây kim loại: e= Blvsin\(\alpha\) với anpha (B,v) = 90 độ
vmax = \(\sqrt{gl}\alpha_0\) = 0,21 m/s
suy ra emax = Blvmax = 0,021 V
-em tham khảo trên mạng dạng bài tương tự thì thấy có ghi
e=\(\frac{Bl^2w}{2}\)
emax khi wmax suy ra wmax=\(\frac{v_{max}}{R}=\frac{\sqrt{2gl\left(1-cos\alpha_0\right)}}{l}\) thay số tính ra e = 10,5 mV
Vậy cách làm nào mới đúng vậy thầy.

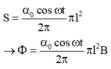
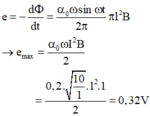
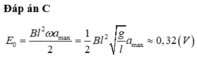
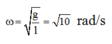
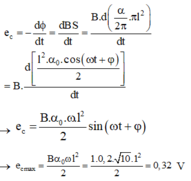
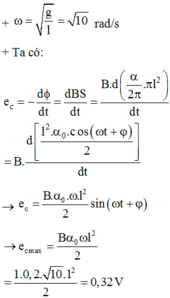
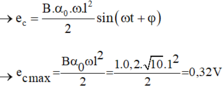
Cách thứ 2 mới đúng em nhé.
Cách 1 chỉ đúng khi dây kim loại chuyển động tịnh tiến, nhưng ở đây là dây kim loại quay quanh 1 đầu cố định.
Mình giải thích thêm về công thức trên như sau.
Ta có suất điện đọng tính bởi :
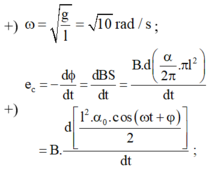
\(e=\dfrac{\Delta\phi}{\Delta t}=\dfrac{B.\Delta S}{\Delta t}=\dfrac{B.\Delta (\dfrac{\alpha}{2\pi}.\pi^2.l )}{\Delta t}=\dfrac{B.\Delta\alpha.l^{2}}{2.\Delta t}=\dfrac{B.l^{2}\omega}{2}\)
Với \(\Delta \alpha\) là góc quay trong thời gian \(\Delta t\) \(\Rightarrow \omega = \dfrac{\Delta \alpha}{\Delta t}\)
\(e_{max}\) khi \(\omega_{max}\), với \(\omega_{max}=\dfrac{v_{max}}{R}=\dfrac{\sqrt{2gl(1-\cos\alpha)}}{l}\)
Thay vào trên ta tìm đc \(e_{max}\)