Cho hình chữ nhật ABCD có phương trình đường thẳng chứa hai cạnh là \(2x-3y+5=0\) và \(3x+2y-7=0\) và đỉnh \(A\left(2;-3\right)\)
Viết phương trình cạnh còn lại ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 3 2018
Ta kiểm tra thấy đỉnh A(7; 4) không nằm trên các đường thẳng d 1 : 7 x − 3 y + 5 = 0 , d 2 : 3 x + 7 y − 1 = 0 nên đây là các cạnh CB, CD. Ta có
S = d A , B C . d A , C D = 7.7 − 3.4 + 5 7 2 + − 3 2 . 3.7 + 7.4 − 1 3 2 + 7 2 = 1008 29
ĐÁP ÁN D
CM
20 tháng 3 2018
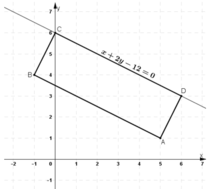
CD: x + 2y – 12 = 0 ⇒ CD nhận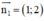 
là một vtpt
⇒ CD nhận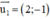 
là một vtcp.
+ ABCD là hcn ⇒ AD ⊥ CD ⇒ AD nhận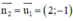 
là một vtpt
A(5 ; 1) ∈ AD
⇒ Phương trình đường thẳng AD: 2( x- 5) – 1(y – 1) = 0 hay 2x – y – 9 = 0.
+ ABCD là hcn ⇒ AB // CD ⇒ AB nhận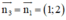 
là một vtpt
A(5;1) ∈ AB
⇒ Phương trình đường thẳng AB: 1( x- 5) + 2(y -1) = 0 hay x + 2y – 7 = 0
+ ABCD là hcn ⇒ BC ⊥ CD ⇒ BC nhận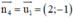 
là một vtpt
C(0, 6) ∈ CD
⇒ Phương trình đường thẳng BC: 2(x- 0)- 1(y – 6) =0 hay 2x – y + 6 = 0.
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2023
Thay tọa độ A vào 2 pt đường thẳng không thỏa mãn, vậy đó là 2 pt đường thẳng của các cạnh BC và CD
\(\Rightarrow\) Khoảng cách từ A đến 2 đường thẳng nói trên bằng độ dài 2 cạnh của hcn
\(\Rightarrow S=d\left(A;\Delta_1\right).d\left(A;\Delta_2\right)=\dfrac{\left|3-2.\left(-1\right)+1\right|}{\sqrt{1^2+\left(-2\right)^2}}.\dfrac{\left|2.3-1\right|}{\sqrt{2^2+1^2}}=6\)
LN
8 tháng 5 2016
\(d\left(I;AB\right)=\frac{\left|\frac{1}{2}+2\right|}{\sqrt{1^2+\left(-2\right)^2}}=\frac{\sqrt{5}}{2}\Rightarrow AD=2d\left(I;AB\right)=\sqrt{5}\)và \(AB=2AD=2\sqrt{5}\)
Do đó \(IA=IB=IC=ID=\frac{1}{2}AC=\frac{5}{2}\)
Gọi \(\omega\) là đường tròn tâm I, bán kính \(R=IA\) thế thì \(\omega\) có phương trình \(\left(x-\frac{1}{2}\right)^2+y^2=\frac{25}{4}\)
Do vậy tọa độ của A, B là nghiệm của hệ :
\(\begin{cases}\left(x-\frac{1}{2}\right)^2+y^2=\frac{25}{4}\\x-2y+2=0\end{cases}\)
Giải hệ thu được \(A\left(-2;0\right);B\left(2;2\right)\) (do A có hoành độ âm), từ đó , do I là trung điểm của AC và BD suy ra \(C\left(3;0\right);D\left(-1;-2\right)\)
CM
10 tháng 2 2018
Ta thấy: điểm A không thuộc hai đường thẳng trên.
Độ dài hai cạnh kề của hình chữ nhật bằng khoảng cách từ A đến hai đường thẳng trên.
Độ dài 2 cạnh là:
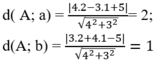
do đó diện tích hình chữ nhật bằng : S= 2.1= 2
Chọn B.
DM
30 tháng 3 2017
Ta có: ABCD là hình chữ nhật nên AB // CD.
Khi đó AB có phương trình: x + 2y + m = 0
Mà A(5; 1) ∈ AB nên m = -7.
Vậy AB có phương trình: x + 2y – 7 = 0
Mặt khác AD ⊥ AB nên AD có phương trình là: 2x – y + n = 0
Mà A ∈ AD nên n = -9.
Vậy AD có phương trình: 2x – y – 9 = 0.
Vì BC // AD nên BC có phương trình: 2x – y + p = 0.
Mà C ∈ BC nên p = 6
Vậy CB có phương trình 2x – y + 6 = 0.
AH
Akai Haruma
Giáo viên
30 tháng 1 2021
Lời giải:
$BD: x+2y-7=0; AD: x+3y-3=0$ nên $D$ chính là giao điểm của 2 PTĐT này.
\(\Rightarrow \left\{\begin{matrix} x_D+2y_D-7=0\\ x_D+3y_D-3=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_D=15\\ y_D=-4\end{matrix}\right.\)
Vì $ABCD$ là hình thoi nên $AC\perp BD$.
$\Rightarrow \overrightarrow{AC}=\overrightarrow{n_{BD}}=(1,2)$
$\Rightarrow \overrightarrow{n_{AC}}=(-2,1)$
PTĐT $AC$ là:
$-2(x-0)+1(y-1)=0\Leftrightarrow -2x+y-1=0\Leftrightarrow 2x-y+1=0$
Gọi $O$ là giao 2 đường chèo $AC, BD$.
\(\Rightarrow \left\{\begin{matrix} 2x_O-y_O+1=0\\ x_O+2y_O-7=0\end{matrix}\right.\Rightarrow \left\{\begin{matrix} x_O=1\\ y_O=3\end{matrix}\right.\)
$O$ là trung điểm $BD$ nên: $x_B=2x_O-x_D=2-15=-13$
$y_B=2y_O-y_D=6+4=10$
Vì $\overrightarrow{BC}=\overrightarrow{AD}$ nên PTĐT $BC$ có dạng:
$(x+13)+3(y-10)-3=0$
$\Leftrightarrow x+3y-30=0$
$O$ là trung điểm của $AC$ nên:
$x_C=2x_O-x_A=2-0=2$
$y_C=2y_C-y_A=6-1=5$
$\Rightarrow \overrightarrow{CD}=(13, -9)$
$\Rightarrow \overrightarrow{n_{CD}}=(9,13)$
PTĐT $CD$ là: $9(x-2)+13(y-5)=0\Leftrightarrow 9x+13y-83=0$
PTĐT $AB$ là: $9(x-0)+13(y-1)=0\Leftrightarrow 9x+13y-13=0$
CM
16 tháng 3 2019
Ta thấy điểm A không thuộc 2 đường thẳng đã cho.
Khoảng cách từ A đến 2 đường thẳng là:
Đáp án B
9 tháng 5 2016
cạnh thứ ba 2x-5y+3=0. cạnh thứ tư 2x-5y-26=0, đường chéo thứ hai 7x-3x-33=0
Từ giả thiết suy ra điểm A không nằm trên 2 cạnh có phương trình đã cho. Bởi vậy, đó là phương trình của 2 đường thẳng chứa cạnh BC, CD, chẳng hạn \(BC:2x-3y+5\)
\(CD:3x+2y-7=0\)
Khi đó, đường thẳng chứa cạnh AB đi qua \(A\left(2;-3\right)\) và song song với đường thẳng CD, nên có phương trình :
\(3\left(x-2\right)+2\left(y+3\right)=0\)
hay : \(3x+2y=0\) ẳng chứa cạnh AD là :
\(2x-3y-11=0\)