Cho tam giác abc.từ điểm D trên cạnh AB kẻ đường thẳng song song với BC cắt AC ở E.Cmr:
a.AD/AB=AE/AC
b.AD/AB=DE/BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 6 2023
a: Xét ΔABC có DE//BC
nên DE/BC=AD/AB
=>DE/10=3/5
=>DE=6cm
b: Xét ΔADE và ΔCGE có
góc AED=góc CEG
góc EAD=góc ECG
=>ΔADE đồng dạng với ΔCGE
c: Xét tứ giác DBCG có
DG//BC
DB//CG
=>DBCG là hình bình hành
=>DB=CG
CM
21 tháng 4 2019
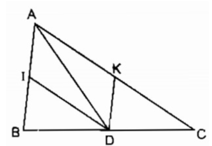
Để hình bình hành AIDK là hình thoi.
⇒ AD là đường phân giác của ∠ (IAK)
hay AD là đường phân giác của ∠ (BAC)
Ngược lại nếu AD là tia phân giác của ∠ (BAC)
Ta có tứ giác AIDK là hình bình hành có đường chéo AD là phân giác của góc A nên tứ giác AIDK là hình thoi
Vậy hình bình hành AIDK là hình thoi khi và chỉ khi D là giao điểm tia phân giác của góc A và cạnh BC.
26 tháng 2 2022
a: Xét ΔABC có DE//BC
nên AD/AB=DE/BC
=>DE/10=3/5
hay DE=6(cm)
b: Xét ΔADE và ΔCGE có
\(\widehat{ADE}=\widehat{CGE}\)
\(\widehat{AED}=\widehat{CEG}\)
Do đó: ΔADE\(\sim\)ΔCGE
Suy ra: AD/CG=AE/CE
hay \(AD\cdot CE=AE\cdot CG\)
Xét ΔABC có DE//BC
nên AD/AB=AE/AC(Định lí Ta lét)
XétΔABC có DE//BC
nên AD/AB=DE/BC(Hệ quả định lí Ta lét)