Cho hàm số \(y=\frac{3x+4}{3x+3}\) có đồ thị (C). Tìm các giá trị tham số m để đường thẳng d : y = x + m cắt đồ thị (C) tại hai điểm phân biệt A và B sao cho tam giác OAB đều ( với O là gốc tọa độ)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 3 2019
Đáp án D
Phương trình hoành độ giao điểm của C và d là
x x − 1 = m − x ⇔ x ≠ 1 x 2 − m x + m = 0 * .
Để C cắt d tại hai điểm phân biệt ⇔ * có hai nghiệm phân biệt khác 1 ⇔ m > 4 m < 0 .
Khi đó, gọi điểm A x 1 ; m − x 1 và B x 2 ; m − x 2 là giao điểm của đồ thị C và d .
⇒ O A = 2 x 1 2 − 2 m . x 1 + m 2 = 2 x 1 2 − m x 1 + m + m 2 − 2 m = m 2 − 2 m O B = 2 x 2 2 − 2 m . x 2 + m 2 = 2 x 2 2 − m x 2 + m + m 2 − 2 m = m 2 − 2 m
Khoảng cách từ O đến AB bằng
h = d O ; d = m 2 ⇒ S Δ A B C = 1 2 . h . A B = m 2 2 . A B
Ta có
S Δ A B C = a b c 4 R ⇔ R = a b c 4. S Δ A B C = O A . O B . A B 2. h . A B = O A . O B 2. h ⇔ 4 2 . m 2 = O A . O B ⇔ O A 2 . O B 2 = 16 m 2
Khi đó m 2 − 2 m 2 = 16 m 2 ⇔ m 2 − 2 m = 4 m m 2 − 2 m = − 4 m ⇔ m = 0 m = − 2 m = 6 .
Kết hợp với điều kiện m > 4 m < 0 , ta được m = − 2 m = 6 là giá trị cần tìm
CM
23 tháng 12 2017
Đáp án B
Phương trình hoành độ giao điểm của (C) và d:
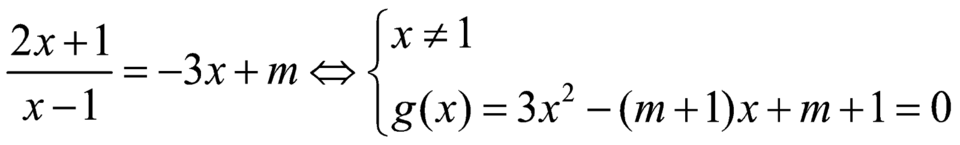
Khi đó d cắt (C) tại hai điểm phân biệt A và B 
(*)
Gọi G là trọng tâm của tam giác OAB ta có O G → = 2 3 O I ⇀ với I là trung điểm của AB.
Tìm được 
Do đó, 
Chú ý: Để làm bài này khi thực hiện trắc nghiệm, ta nên tìm đến điều kiện (*), sau đó loại các kết quả 
và 
Sau đó, lấy một giá trị nguyên của m để kiểm tra giả thiết bài cho, giả sử với m = -2.
Ta còn lại đáp số của bài toán.
CM
24 tháng 2 2019
Chọn D.
Phương pháp:
Giải phương trình hoành độ giao điểm, tìm giao điểm của hai đồ thị.
Dựa vào công thức trọng tâm, xác định m.
Cách giải:
Phương trình hoành độ giao điểm của d và (C) là
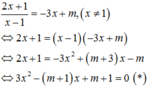
Để d cắt (C) tại hai điểm phân biệt A, B thì (*) có 2 nghiệm phân biệt khác 1
CM
4 tháng 5 2018
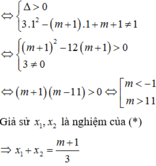
Đáp án C
Phương trình hoành độ của ( C ) và ( d ) là
2 x + 1 x − 1 = m − 3 x ⇔ x ≠ 1 3 x 2 − m + 1 x + m + 1 *
Để ( C ) cắt ( d ) tại 2 điểm phân biệt ⇔ * có 2 nghiệm phân
biệt khác 1 ⇔ m > 11 m < − 1 .
Khi đó, gọi A x 1 ; y 1 , B x 2 ; y 2 là tọa độ giao điểm
⇒ G x 1 + x 2 3 ; y 1 + y 2 3 Mà
y 1 = − 3 x 1 + m y 2 = − 3 x 2 + m ⇒ y 1 + y 2 3 = 2 m − 3 x 1 + x 2 3 = m − 1 3 ⇒ G m + 1 9 ; m − 1 3 .
Theo bài ra, ta có
G ∈ C s u y r a m − 1 3 . m + 1 9 − 1 = 2. m + 1 9 + 1 ⇒ m = 15 ± 5 13 2 .
Kết hợp với điều kiện
m > 11 m < − 1 ⇒ m = 15 + 5 13 2 .
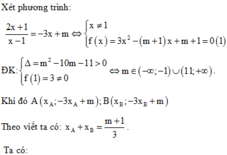
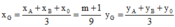
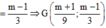
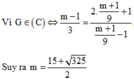
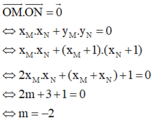
Phương trình hoành độ giao điểm \(3x^2+2mx+3m-4=0\left(1\right)\) với x. Đường thẳng d cắt đồ thị (C) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\begin{cases}9m^2-36m+48>0\\0.m-1\ne0\end{cases}\) (đúng với mọi m)
Gọi \(x_1;x_2\) là các nghiệm của phương trình (1), ta có : \(\begin{cases}x_1+x_2=-m\\x_1x_2=\frac{3m-4}{3}\end{cases}\) (*)
Giả sử \(A\left(x_1;x_1+m\right);B\left(x_2;x_2+m\right)\)
Khi đó ta có \(OA=\sqrt{x^2_1+\left(x_1+m\right)^2};OA=\sqrt{x^2_2+\left(x_2+m\right)^2}\)
Kết hợp (*) ta được \(OA=OB=\sqrt{x_1^2+x_2^2}\)
Suy ra tam giác OAB cân tại O
Ta có \(AB=\sqrt{2\left(x_1-x_2\right)^2}\). Tam giác OAB đều \(\Leftrightarrow OA^2=AB^2\Leftrightarrow x_1^2+x_2^2=2\left(x_1-x_2\right)^2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-6x_1x_2=0\)
\(\Leftrightarrow m^2-6m+8=0\Leftrightarrow m=2\) hoặc m=4