Trong quang phổ của nguyên tử hiđrô , nếu biết bước sóng dài nhất của vạch quang phổ trong dãy Lai-man là\(\lambda_1\)và bước sóng của vạch kề với nó trong dãy này là \(\lambda_2\) thì bước sóng \(\lambda_{\alpha}\) của vạch quang phổ \(H_{\alpha}\)trong dãy Ban-me là
A.\(\frac{\lambda_1\lambda_2}{\lambda_1-\lambda_2}.\)
B.\(\lambda_1-\lambda_2.\)
C.\(\frac{\lambda_1\lambda_2}{\lambda_1+\lambda_2}.\)
D.\(\lambda_1+\lambda_2.\)

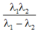
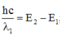
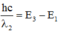
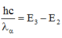
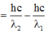
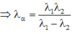
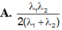
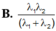
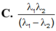
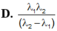
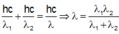
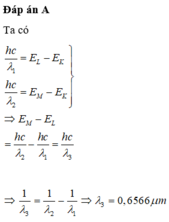
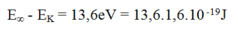
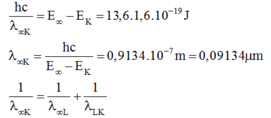
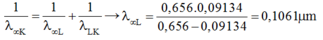
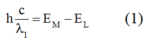
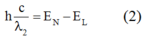
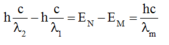
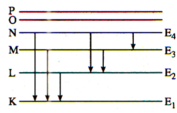
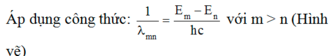
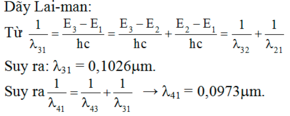
Bước sóng dài nhất của vạch quang phổ trong dãy Lai-man thu được khi nguyên tử nhảy từ L về K. Khi đó \(\lambda_1\) thỏa mãn: \(hf_1=\frac{hc}{\lambda_1}= E_2-E_1,(1)\)
Bước sóng \(\lambda_2\)của vạch kề với \(\lambda_1\) thu được khi nguyên tử nhảy từ M về K.
Khi đó \(\lambda_2\) thỏa mãn: \(hf_2=\frac{hc}{\lambda_2}= E_3-E_1,(2)\)
Bước sóng \(\lambda_{\alpha}\) trong vạch quang phổ \(H_{\alpha}\) trong dãy Ban-me thu được khi nguyên tử nhảy từ M về L.
Khi đó \(\lambda_{\alpha}\) thỏa mãn: \(hf_{\alpha}=\frac{hc}{\lambda_{\alpha}}= E_3-E_2,(3)\)
Trừ (2) cho (1) thu được (3):
\(\frac{hc}{\lambda_{2}}-\frac{hc}{\lambda_{1}}= \frac{hc}{\lambda_{\alpha}}\)=> \( \frac{1}{\lambda_{\alpha}}=\frac{1}{\lambda_{2}}-\frac{1}{\lambda_{1}}\)
=> \(\lambda_{\alpha}=\frac{\lambda_1\lambda_2}{\lambda_1-\lambda_2}.\)