Tính
a) cos2250 , sin2400 , cot(-150 ), tan 750 ;
b) sin, cos
, tan
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A,xem lại đề
B\(=sin^6x+cos^6x+3sin^2x.cos^2x\)
\(=\left(sin^2x\right)^3+3sin^2x.cos^2x\left(sin^2x+cos^2x\right)+\left(cos^2x\right)^3\)
\(=\left(sin^2+cos^2x\right)^3\)
\(=1\)
a) Sửa đề: \(A=\cot48^0\cdot\cot42^0+\tan60^0\)
Ta có: \(A=\cot48^0\cdot\cot42^0+\tan60^0\)
\(=\cot48^0\cdot\tan48^0+\tan60^0\)
\(=1+\sqrt{3}\)

khai triển hằng đẳng thức : kết quả quả còn lại 4. căn (tanB.cot B) = 4 ( vì tanB.cotB = 1 )
\(\left(a+b\right)^2-\left(a-b\right)^2=4ab\)
Nên ta có:
\(\left(\tan\beta+\cot\beta\right)^2-\left(\cot\beta-\tan\beta\right)^2=4\cdot\tan\beta\cdot\cot\beta=4\forall\beta\).ĐPCM
tan(x)*cot(x) = 1 với mọi x.

\(\left(tan\alpha+cot\alpha\right)^2-\left(cot\alpha-tan\alpha\right)^2=\left(tan\alpha+cot\alpha-cot\alpha+tan\alpha\right)\left(tan\alpha+cot\alpha+cot\alpha-tan\alpha\right)=4tan\alpha.cot\alpha=4\)

- sin 45 = cos 45 => sin 45 - cos 45 =0 => A =0
- sin 45 = cos 45 ; tan 45 = cot 45 => \(\frac{sina-tana}{cota-cosa}=\frac{sina-tana}{tana-sina}=-1\)

\(\tan\alpha+\cot\alpha=2\Leftrightarrow\tan\alpha+\frac{1}{\tan\alpha}=2\)
\(\Rightarrow\tan^2\alpha+1=2\tan\alpha\)
\(\Leftrightarrow\tan\alpha=1\Rightarrow\alpha=45\)

\(\tan\alpha+\cot\alpha=1\)\(1\)\(\Rightarrow\hept{\begin{cases}\tan\alpha=1\\\cot\alpha=1\end{cases}}\)\(\Rightarrow\alpha=45\)độ
a) + cos2250 = cos(1800 + 450 ) = -cos450 =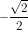
+ sin2400 = sin(1800 + 600 ) = -sin600 =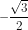
+ cot(-150 ) = -cot150 = -tan750 = -tan(300 + 450 )
= -2 - √3
+ tan 750 = cot150= 2 + √3
b)
+ sin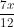 = sin
= sin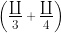 = sin
= sin cos
cos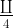 + cos
+ cos sin
sin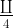
+ cos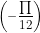 = cos
= cos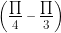 = cos
= cos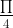 cos
cos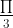 + sin
+ sin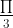 sin
sin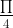
+ tan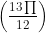 = tan(π +
= tan(π + 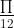 ) = tan
) = tan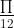 = tan
= tan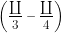 =
= 
= 2 - √3