Giải phương trình :
\(3^{\cos x}-2^{\cos x}=\cos x\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với \(cosx=0\) ko phải nghiệm
Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)
\(\Rightarrow tan^2x-4\sqrt{3}tanx+1=-2\left(1+tan^2x\right)\)
\(\Leftrightarrow3tan^2x-4\sqrt{3}tanx+3=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=\sqrt{3}\\tanx=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\\x=\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)


Đáp án D
Ta có
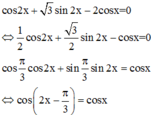
Do đó để phương trình ![]() tương đương với phương trình
tương đương với phương trình
![]()

Xét hàm số \(f\left(t\right)=t^{\cos\alpha}-t\cos\alpha\)
Ta có : \(f'\left(x\right)=\left(t^{\cos\alpha}-1\right)\cos\alpha\)
Khi đó \(f\left(3\right)=f\left(2\right)\) và \(f\left(1\right)\) khả vi liên tục trên \(\left[2;3\right]\) Theo định lí Lagrange thì tồn tại \(c\in\left[2;3\right]\) sao cho :
\(f'\left(c\right)=\frac{f\left(3\right)-f\left(2\right)}{3-2}\) hay \(\left(c^{\cos\alpha-1}-1\right)\cos\alpha\)
Từ đó suy ra :
\(\begin{cases}\cos\alpha=0\\\cos\alpha=1\end{cases}\)\(\Leftrightarrow\begin{cases}\alpha=\frac{\pi}{2}+k\pi\\\alpha=k\pi\end{cases}\) \(\left(k\in Z\right)\)
Thử lại ta thấy các giá trị này đều thỏa mãn
Vậy nghiệm của phương trình là \(x=\frac{\pi}{2}+k\pi;x=k\pi\) và \(\left(k\in Z\right)\)