Cho tam giác ABC. Xét các điểm M thuộc BC, N thuộc CA và P thuộc AB sao cho tứ giá APMN là một hình bình hành. Các đường thẳng BN và CP cắt nhau tại O. Chứng minh rằng đường thẳng OM luôn đi qua 1 điểm cố định.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi D là đỉnh thức tư của hình bình hành ABDC. Khi đó, O, M, D thẳng hàng.
Do giả thiết nên DB//MP, DC//MN. Từ đó, do O, M, D thẳng hàng, nên góc PMO = góc OMN <=> OM là phân giác góc PMN <=> DM là phân giác góc BDC
\(\Leftrightarrow\frac{MB}{MC}=\frac{DB}{DC}\)
Nhưng tứ giác ABDC là một hình bình hành nên BD = AC, CD = AB
do đó : \(\frac{DB}{DC}=\frac{AC}{AB}\)
Vì vậy :
góc PMO bằng góc OMN \(\Leftrightarrow\frac{MB}{MC}=\frac{AC}{AB}\)
Vậy với M là điểm trên cạnh BC sao cho \(\frac{MB}{MC}=\frac{AC}{AB}\) (hay M đối xứng với chân phân giác trong góc BAC qua trung điểm cạnh BC) thì góc PMO bằng góc OMN => Điều cần chứng minh

a) Ta chứng minh A N = C M A N ∥ C M ⇒ A M C N là hình bình hành.
Vì O là giao điểm của AC và BD, ABCD là hình chữ nhật nên O là trung điểm AC
Do ANCM là hình bình hành có AC và MN là hai đường chéo
⇒ O là trung điểm MN
b. Ta có: EM//AC nên E M D ^ = A C D ^ (2 góc so le trong)
NF//AC nên B N F ^ = B A C ^ (2 góc so le trong)
Mà A C D ^ = B A C ^ (vì AB//DC, tính chất hình chữ nhật)
⇒ E M D ^ = B N F ^
Từ đó chứng minh được ∆ E D M = ∆ F B N ( g . c . g )
⇒ E M = F N
Lại có EM//FN (vì cùng song song với AC)
Nên tứ giác ENFM là hình bình hành
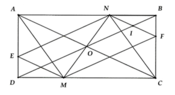
c) Tứ giác ANCM là hình thoi Û AC ^ MN tại O Þ M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.
Khi đó M và N là trung điểm của CD và AB.
d) Ta chứng minh được DBOC cân tại O ⇒ O C B ^ = O B C ^ v à N F B ^ = O C F ^ (đv) Þ DBFI cân tại I Þ IB = IF (1)
Ta lại chứng minh được DNIB cân tại I Þ IN = IB (2)
Từ (1) và (2) Þ I là trung điểm của NF.

a) Tứ giác ACEH có
ˆACE=ˆEHA=900ACE^=EHA^=900(cùng nhìn AE)
=> tứ giác ACHE nội tiếp
b) tứ giác ACHE nội tiếp
=> ˆEAH=ˆHCEEAH^=HCE^(cùng chắn EH)
lại có ˆADF=ˆACFADF^=ACF^(cùng chắn AF)
mà ˆACF+ˆHCE=900ACF^+HCE^=900do ˆACE=900ACE^=900
=>ˆEAH+ˆADF=900EAH^+ADF^=900
=> DF⊥ABDF⊥AB
mà EH⊥ABEH⊥AB
=> DF//EHDF//EH
c)các bước chứng minh nè :
cm HOD=DCH (2 góc cùng nhìn DH)
thì => COHD nọi tiếp đường tròn thì đường tròn sẽ đi qau C H O D

a) Tứ giác ACEH có
\(\widehat{ACE}=\widehat{EHA}=90^0\)(cùng nhìn AE)
=> tứ giác ACHE nội tiếp
b) tứ giác ACHE nội tiếp
=> \(\widehat{EAH}=\widehat{HCE}\)(cùng chắn EH)
lại có \(\widehat{ADF}=\widehat{ACF}\)(cùng chắn AF)
mà \(\widehat{ACF}+\widehat{HCE}=90^0\)do \(\widehat{ACE}=90^0\)
=>\(\widehat{EAH}+\widehat{ADF}=90^0\)
=> \(DF\perp AB\)
mà \(EH\perp AB\)
=> \(DF//EH\)
c)các bước chứng minh nè :
cm HOD=DCH (2 góc cùng nhìn DH)
thì => COHD nọi tiếp đường tròn thì đường tròn sẽ đi qau C H O D

Đặt \(\overrightarrow{AB}=\overrightarrow{b}\), \(\overrightarrow{AC}=\overrightarrow{c}\)
Do B. M, C thẳng hàng theo thứ tự, nên tồn tại n, p > 0 sao cho \(\overrightarrow{AM}=n\overrightarrow{c}+p\overrightarrow{b}\) với \(n+p=1\)
Từ đó, do tứ giác ANMP là hình bình hành, nên \(\overrightarrow{AP}=p\overrightarrow{b}\), \(\overrightarrow{AN}=n\overrightarrow{c}\)
Do B, O, N thẳng hàng và C, O, P thẳng hàng nên
\(\overrightarrow{AO}=x\overrightarrow{b}+ny\overrightarrow{c}=z\overrightarrow{c}+pt\overrightarrow{b}\)
trong đó \(x+y=1=z+t\)
Từ đó, do hai vectơ \(\overrightarrow{b},\overrightarrow{c}\) không cùng phương nên \(x=\frac{p\left(1-n\right)}{1-np}\) và \(y=\frac{1-p}{1-np}\)
Do đó :
\(\overrightarrow{AO}=\frac{p\left(1-n\right)}{1-np}.\overrightarrow{b}+\frac{n\left(1-p\right)}{1-np}.\overrightarrow{c}\)
Suy ra :
\(\left(1-np\right).\overrightarrow{OM}=\left(1-np\right)\left(\overrightarrow{AM}-\overrightarrow{AO}\right)=np\left(1-p\right)\overrightarrow{b}+np\left(1-n\right)\overrightarrow{c}\)
\(\Rightarrow\frac{1-np}{np}.\overrightarrow{OM}=\left(\overrightarrow{b}+\overrightarrow{c}\right)-\left(n\overrightarrow{c}+p\overrightarrow{b}\right)\)
Hay
\(\overrightarrow{AM}=np\overrightarrow{AD}+\left(1-np\right)\overrightarrow{AO}\)
Trong đó D là điểm thỏa mãn \(\overrightarrow{AD}=\overrightarrow{b}+\overrightarrow{c}\) Từ đó, đường thẳng OM luôn đi qua D cố định (D là đỉnh thứ tư của hình bình hàng ABDC)