Một vật bắt đầu chuyển động thẳng nhanh dần đều từ trạng thái đứng yên. Khi đạt tới vận tốc cực đại nó chuyển sang chuyển động chậm dần đều cho tới khi dừng hẳn. Biết độ dài của "đoạn đường hãm" lớn gấp 2 lần đoạn đường tăng tốc. Tìm tỉ số gia tốc và tỉ số thời gian chuyển động trên hai đoạn đường đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 7 2016
Vật chuyển động từ trạng thái nghỉ đến vận tốc cực đại \(v_0\)
áp dụng công thức của chuyển động biến đổi đều ta có
\(2a_1s_1=v^2_0\)
Trong quá trình giảm dần đều ta cũng có
\(2a_2s_2=v^2_0\)
Theo đầu bài cho \(s_2=2s_1\) dẫn đến \(a_1=2a_2\)
Và thời gian \(\Delta t_2=2\Delta t_1\)
TK
23 tháng 10 2021
Ta có
\(s_1+s_2=\dfrac{v_1^2}{2a_1}+\dfrac{-v_1^2}{2a_2}=\dfrac{v_1^2}{2\cdot2}+\dfrac{-v_1^2}{2\cdot\left(-2,5\right)}=180\Rightarrow v_1=20\left(\dfrac{m}{s}\right)\)
Quãng đường chuyển động của xe trong từng giai đoạn
\(s_1=\dfrac{v_1^2}{2\cdot a_1}=\dfrac{20^2}{2\cdot2}=100\left(m\right);s_2=\dfrac{-v_1^2}{2\cdot a_2}=-\dfrac{20^2}{2\cdot\left(-2,5\right)}=80\left(m\right)\)
Thời gian qua từng giai đoạn
\(t_1=\sqrt{\dfrac{2s_1}{a_1}}=10\left(s\right);t_2=\sqrt{\dfrac{2s_2}{a_2}}=8\left(s\right)\)
23 tháng 9 2021
5) Đổi 36km/h = 10m/s
Gia tốc của tàu:
Ta có: \(v=v_0+at\Leftrightarrow a=\dfrac{v-v_0}{t}=\dfrac{0-10}{5}=-2\left(m/s^2\right)\)
Quãng đường đi đc:
\(s=v_0t+\dfrac{1}{2}at^2=10.5+\dfrac{1}{2}.\left(-2\right).5^2=25\left(m\right)\)
23 tháng 9 2021
6)
a) Gia tốc của vật:
Ta có: \(v^2-v^2_0=2as\Leftrightarrow a=\dfrac{v^2-v^2_0}{2s}=\dfrac{10^2-0^2}{2.100}=0,5\left(m/s^2\right)\)
b) Quãng đường vật đi đc:
\(s=v_0t+\dfrac{1}{2}at^2=0.5+\dfrac{1}{2}.0,5.5^2=6,25\left(m\right)\)
Vận tốc của vật khi đó:
\(v=v_0+at=0+0,5.5=2,5\left(m/s\right)\)
VT
22 tháng 9 2017
Đáp án C
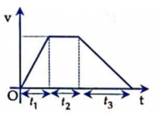
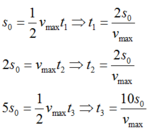
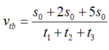
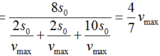
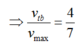
Chú ý: Vật chuyển động gồm ba giai đoạn (như hình vẽ): nhanh dần – đều – chậm dần đều ta có công thức
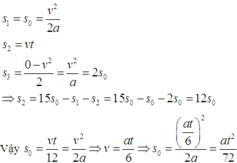
Vật chuyển động từ trạng thái nghỉ đến vận tốc cực đại \(v_0\)
áp dụng công thức của chuyển động biến đổi đều ta có
\(2a_1s_1=v^2_0\)
Trong quá trình giảm dần đều ta cũng có
\(2a_2s_2=v^2_0\)
Theo đầu bài cho \(s_2=2s_1\) dẫn đến \(a_1=2a_2\)
Và thời gian \(\Delta t_2=2\Delta t_1\)