Bài 1: Tứ giác ABCD có Â =C. Chứng minh rằng các đường phân giác của góc B và góc D song song với nhau hoặc trùng nhau
Bài 2: Chứng minh rằng trong một tứ giác tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 7 2019
Bài 1)
Trên AD lấy E sao cho AE = AB
Xét ∆ACE và ∆ACB ta có :
AC chung
DAC = BAC ( AC là phân giác)
AB = AE (gt)
=> ∆ACE = ∆ACB (c.g.c)
=> CE = CB (1)
=> AEC = ABC = 110°
Mà AEC là góc ngoài trong ∆EDC
=> AEC = EDC + ECD ( Góc ngoài ∆ bằng tổng 2 góc trong không kề với nó)
=> ECD = 110 - 70
=> EDC = 40°
Xét ∆ EDC :
DEC + EDC + ECD = 180 °
=> CED = 180 - 70 - 40
=> CED = 70°
=> CED = EDC = 70°
=> ∆EDC cân tại C
=> CE = CD (2)
Từ (1) và (2) :
=> CB = CD (dpcm)
b) Ta có thể thay sao cho tổng 2 góc đối trong hình thang phải = 180°
CM
22 tháng 2 2019
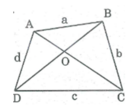
Đặt độ dài a = AB, b = BC, c = CD, d = AD
Gọi O là giao điểm 2 đường chéo AC và BD.
* Trong ∆ OAB, ta có:
OA + OB > a (bất đẳng thức tam giác) (1)
* Trong ∆ OCD, ta có:
OC + OD > c (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra:
OA + OB + OC + OD > a + c hay AC + BD > a + c (*)
* Trong ∆ ΔOAD, ta có: OA + OD > d (bất đẳng thức tam giác) (3)
* Trong ∆ OBC, ta có: OB + OC > b (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra:
OA + OB + OC + OD > b + d hay AC + BD > b + d (**)
Từ (*) và (**) suy ra: 2(AC + BD) > a + b + c + d
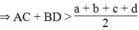
* Trong ∆ ABC, ta có: AC < AB + BC = a + b (bất đẳng thức tam giác)
* Trong ∆ ADC, ta có: AC < AD + DC = c + d (bất đẳng thức tam giác)
Suy ra: 2AC < a + b + c + d
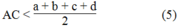
* Trong ∆ ABD, ta có: BD < AB + AD = a + d (bất đẳng thức tam giác)
* Trong ∆ BCD, ta có: BD < BC + CD = b + c (bất đẳng thức tam giác)
Suy ra: 2BD < a + b + c + d
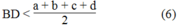
Từ (5) và (6) suy ra: AC + BD < a + b + c + d
1: