Tìm abc biết : ab + bc + ca
giải chi tiết
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MK
0
MK
1
LQ
6 tháng 12 2015
abc = 22 x (a+b+c)
abc chia hết cho 22, tức là chia hết cho 2 và chia hết cho 11
vậy c = 0,2,4,6,8.
a+c-b chia hết 11
a+b+c tối đa là 27 nên 22 x 27 = 594 vậy a < 5
a+b+c nhỏ nhất là 5
c lớn nhất là 8, a nhỏ hơn 5 nên tổng a+b+c lớn nhất chỉ : 9+5+8=22.
a=4,3,2,1
xét các trường hợp :
a=1 vậy có thể là: 154, 176, 198
a=2 vậy có thể là: 264, 286
a=3 vậy có thể là : 352, 374, 396
a=4 vậy có thể là: 440,462
ĐÁP SỐ : 264
MK
0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 6 2023
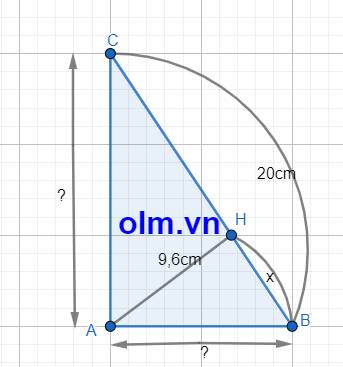
Gọi độ dài đoạn BH là: \(x\) ( cm) ; \(x\) > 0; AC > AB nên \(x\) < CH
Xét tam giác vuông HAB vuông tại H theo pytago ta có:
AB2 = HA2 + HB2 = 9,62 + \(x^2\) = 92,16 + \(x^2\)
Xét tam giác vuông AHC vuông tại H theo pytago ta có:
AC2 = HA2 + HC2 = 9,62 + (\(20-x\))2 = 92,16 + 400 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(x\) + \(x^2\)
Xét tam giác vuông ABC vuông tại A theo pytago ta có:
AC2 + AB2 = BC2
492,16 - 40\(x\) + \(x^2\) + 92,16 + \(x^2\) = 202
(\(x^2\) + \(x^2\)) - 40\(x\) + (492,16 + 92,16) - 400 = 0
2\(x^2\) - 40\(x\) + 584,32 - 400 = 0
2\(x^2\)- 40\(x\) + 184,32 =0
\(x^2\) - 20\(x\) + 92,16 = 0
△' = 102 - 92,16 = 7,84 > 0
\(x\)1 = -(-10) + \(\sqrt{7,84}\) = 12,8 ⇒ CH = 20 - 12,8 = 7,2 < BH (loại )
\(x_2\) = -(-10) - \(\sqrt{7,84}\) = 7,2 ⇒ CH = 20 - 7,2 = 12,8 (thỏa mãn)
Thay \(x_2\) = 7,2 vào biểu thức: AB2 = 92,16 + \(x^2\) = 92,16 + 7,22 = 144
⇒AB = \(\sqrt{144}\) = 12
Thay \(x_2\) = 7,2 vào biểu thức: AC2 = 492,16 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(\times\) 7,2 + 7,22 = 256
AC = \(\sqrt{256}\) = 16
Kết luận AB = 12 cm; AC = 16 cm
Q
23 tháng 4 2017
Cách vẽ:
Vẽ AC = 5 cm.
Vẽ cung tròn (A; 3 cm).
Vẽ cung tròn (C; 4 cm).
Hai cung tròn cắt nhau tại B. Vẽ đoạn thẳng BA, BC ta được tam giác ABC.
Tam giác ABC có 1 góc vuông tại B
17 tháng 5 2022
a: \(BC=\sqrt{18^2+12^2}=3\sqrt{61}\left(cm\right)\)
b: Vì G là trọng tâm
và AM là đường trung tuyến
nên AG=2/3AM=10(cm)
Ta có abc= 11x(a+b+c)
=> ax100+bx10+c=11xa+11xb+11xc
=> 89xa=b+10xc
vic b;c lớn nhất là 9 nên a=1
Vì thế b=89-10xc
Vì b không thể mang dấu "-" mà b có một chữ số nên c=8( kết quả 8 là duy nhất)
<=> b= 89-10x8=9
Vậy b=9
=> abc=198
abc = ab + bc + ac
Nếu a = b = c = 0 => thỏa mãn
Nếu a, b, c khác 0
=> Ta có:
1 = (ab + bc + ca)/abc = 1/a + 1/b + 1/c
Vậy {a; b; c} là tập hợp của {2; 3; 6}; {3; 3; 3}